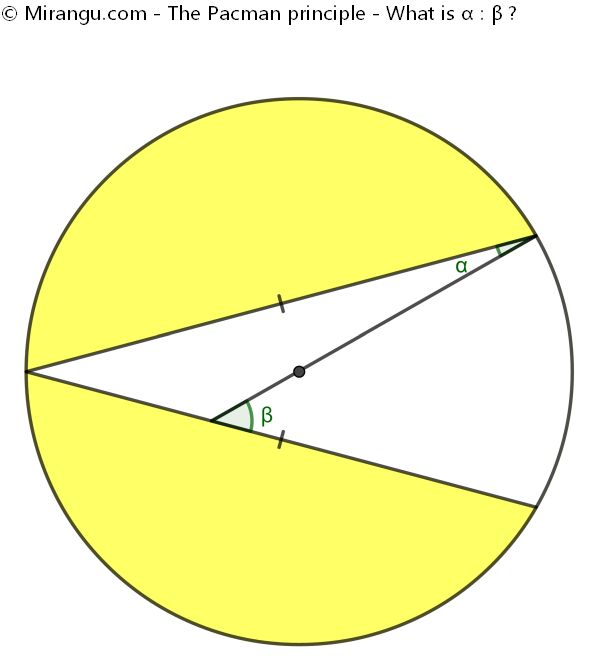
In a circle, two congruent chords are connected in a point. A line segment is drawn through the circle center as shown, forming two angles. What is the proportion α : β?
Scroll down for a solution to this problem.
Solution
The angle proportion α : β is 1 : 3.
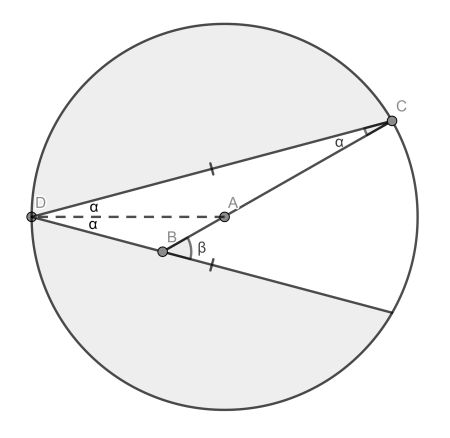
Draw the radius from the meeting point D to the circle centre A. From reflection symmetry in this line, it follows that it is the bisector of the angle formed by the chords. Now from the isosceles triangle DAC it is clear that these halves equal α.
From analysing triangle DBC it follows that angle DBC is 180 – 3α. Hence β=3α.