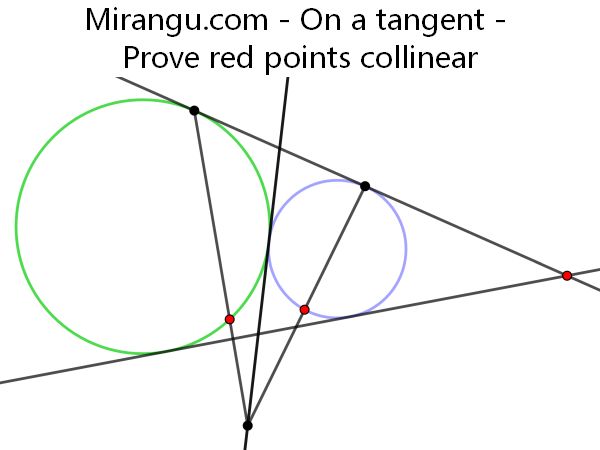
Two tangent circles and their three common tangents. Two secants meet on the internal tangent. Prove that the three red points are collinear.
Scroll down for a solution to this problem.
Solution
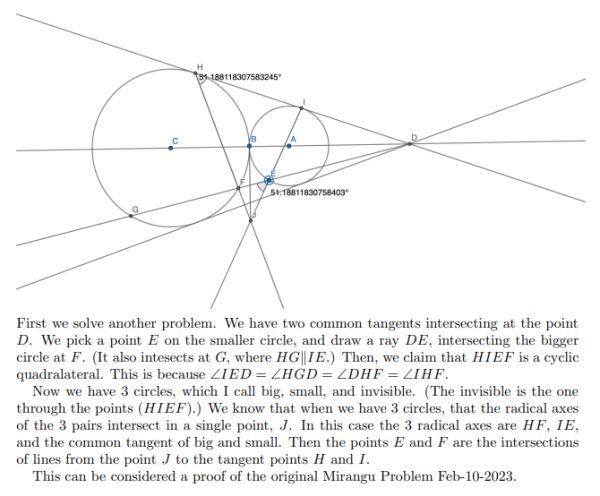
Two tangent circles and their three common tangents. Two secants meet on the internal tangent. Prove that the three red points are collinear.
Scroll down for a solution to this problem.

Two tangent circles and their three common tangents. Two secants meet on the internal tangent. Prove that the three red points are collinear. https://t.co/kBKhV8nx8v Inspired by Posamentier. pic.twitter.com/fwREbQaG44
— Mirangu (@Mirangu1) February 10, 2023
2 replies on “On a tangent”
In the Solution above, I claim that HG is parallel to IE. The way to see that is to use a homothety, dilating about the point D, that expands the small circle into the large circle. Under this homothety, the points I and E on the small circle move to the points H and G, respectively, on the large circle, the secant IE expands to the secant HG, and the secants are parallel.
Ignacio Larrosa Cañestro pointed out that
“If the circles aren’t tangent and the common internal tangent is replaced by their radical axis, the result remains.”
The Solution above also can be used to prove this generalization.
He also pointed out (implicitly) that it is not necessary to invoke the 3 radical axes theorem. Instead, the cyclic quadrilateral condition can be used to show that the intersection point J of the lines HF and IE must have the same power with respect to both the big and small circles, implying the J must be on the radical axis.