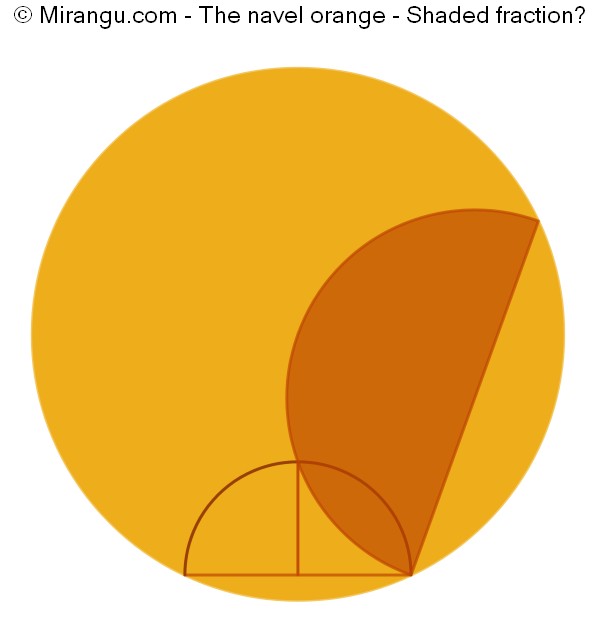
Two quarter circles and a semicircle inside a circle. What fraction of the circle is shaded by the semicircle?
Scroll down for a solution to this problem.
Solution
A fraction of 1/4 is shaded.
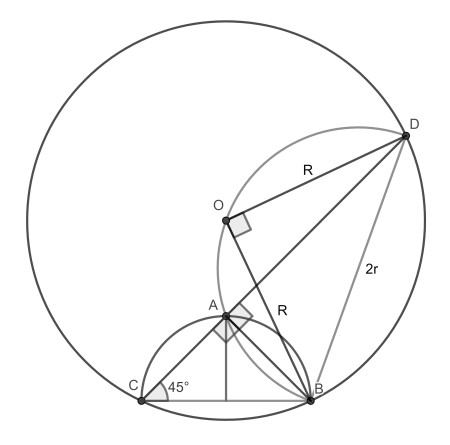
First draw line segments CA, BA and DA. From applying Thales in both semicircles we get two right angles. This implies that CD is a straight line.
From looking at angle DCB of 45° and applying the inscribed angle theorem, we find that angle DOB is right, where O is the circle centre.
From the inverse of Thales we get that O must also lie on the shaded semicircle. Now it is simply applying the Pythagoras theorem to learn that R2=2r2.
Please find here a nice Desmos calculator by Per Henrik Christiansen showing all possible configurations.
Poem
The earth is blue like a orange
Whasps bloom green
A necklace of windows
Wings cover the leaves
You have all the joy of the sun
All the sun on the earth
On the way to your beauty
(translated from a poem from Paul Eluard)