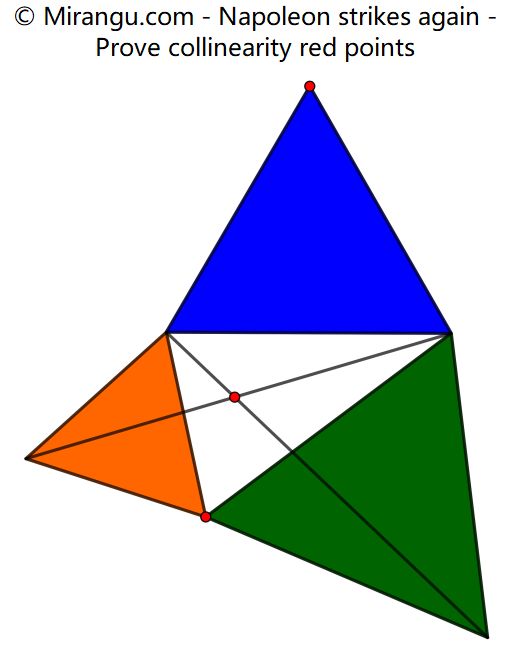
Three equilateral triangles and two line segments. Prove that the three red points are collinear.
Scroll down for a solution to this problem.
Solution
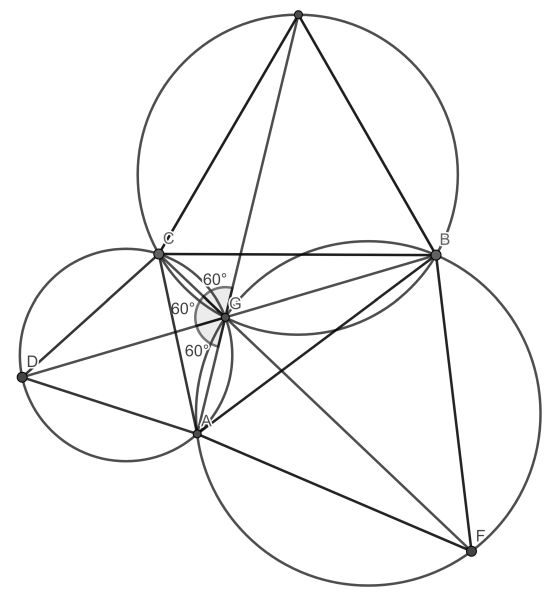
From congruence of triangles CAF and DAB and the fact that ∠DAC is 60° it follows that ∠DGC is 60°. Therefore quadrilateral DAGC is cyclic and so is AFBG. The intersection G is therefore the common point of the three circumcircles of the equilateral triangles.
Now its is seen that the three angles left from G add up to 180° and therefore it is a straight line.
Poem
Napoléon Bonaparte was not only
A military leader
Also a lover of mathematics
And strategic plans
He used the compas
For geometric figures
He liked scientific questions
As well as military instructions
And practical details
He left an immense scientific and political legacy

3 replies on “Napoleon strikes again”
Notice that you can draw the diagram by starting with a Napoleon equilateral triangle ABC and any interior point D, then reflect D outward with respect to the sides of the Napoleon triangle to get three vertices D’, D1′, and D2′. Then the original triangle ABC is the Napoleon triangle of D’ D1′ D2′. Also, the lines D-D’, D-D1′, D-D2′ go through the outside vertices G,E,F of the three colored equilateral triangles built on the sides of triangle D’D1’D2′. The original points A,B,C are the centers of those colored triangles.
The point of intersection is known as Fermat point or Fermat-Toricelli point!
A related problem, which may explain the title of this one, is
“Triangle Quartet II” from August 18, 2021. That one is known as Napoleon’s Theorem.