Two similar triangles inside a semicircle. What’s the angle?
Scroll down for a solution to this problem.
Solution
The angle can be anything between 0° and 45°.
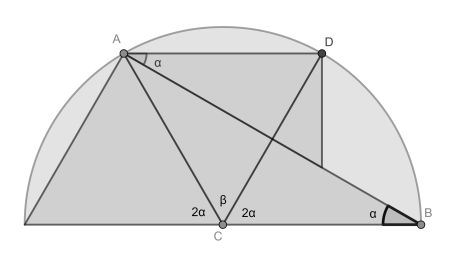
Calling the desired angle α, we can find another α in the small triangle as shown. From Thales we infer two times 2α in the centre.
Now somehow, while drawing the graph, I assumed AB and CD to be perpendicular. In this case they are, but they needn’t be in general. Therefore α is undetermined. See also this Desmos calculator by Per Henrik Christiansen.
If we do assume the extra constraint of perpendicular chord and radius, we can set β=2α and hence 6α=180, leading to α=30°.
