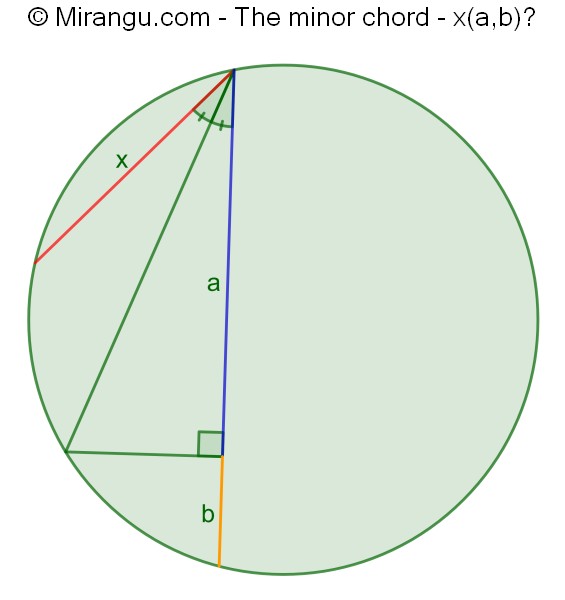
Three chords meet at the same point on the circumference of the circle. A perpendicular line segment divides one of them in two parts of length a and b. Express the length of the smallest chord x in terms of a and b.
Scroll down for a solution to this problem.
Solution
The chord’s length is x=a-b.
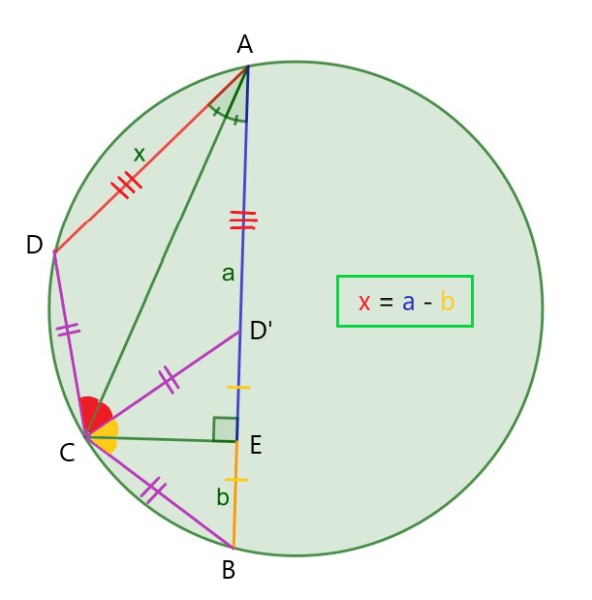
BC = CD. Reflection of D about AC = Reflection of B about CE. Therefore ED’ = b and AD’ = x = a – b.