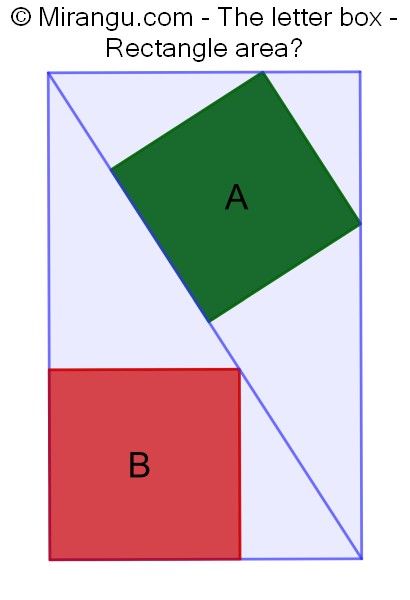
A rectangle with a diameter and two inscribed squares. What is its area in terms of the square areas A and B?
Scroll down for a solution to this problem.
Solution
The rectangle area is B[1+√(B/(B-A))].
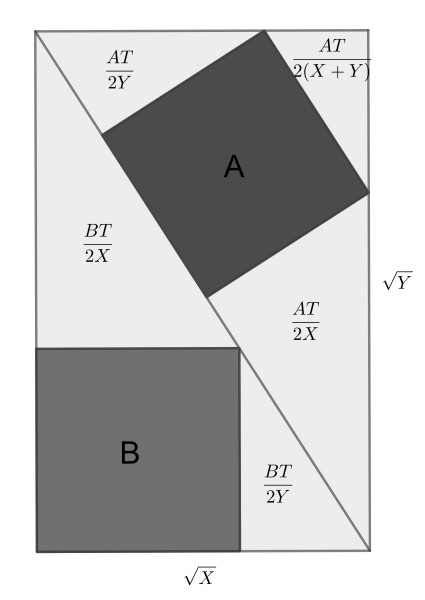
The rectangle side lengths are √X and √Y. The key is that all triangles are similar. It is then a matter of expressing their area in terms of the rectangle area T, as shown in the diagram.
From the lower half of the rectangle we get 1+T/2X+T/2Y=T/2B, whereas the upper half gives 1+T/2X+T/2Y+T/2(X+Y)=T/2A.
Subtracting these equations gives 1/(X+Y)=1/A-1/B, which leads to T2(1/X+1/Y)=AB/(B-A).
Adding the two equations and using the above leads to T2/B-2T-AB/(B-A)=0. This is a quadratic equation in T, which can be solved to find the desired answer.
Poem
The letter box
Is our confidant and our friend
Especially in Xmas Time
All children are writing letters
Children’s love letters
Writing poems
Send drawings
Tell one’s story
Letters to get presents
To see the toys
To see Santas sleigh
The letter box is precious and usefull