Express the circle area in terms of the isosceles triangle area A and its side length a.
Scroll down for a solution to this problem.
Solution
The circle area is πa6/(16A2).
Categories
Launch the ball
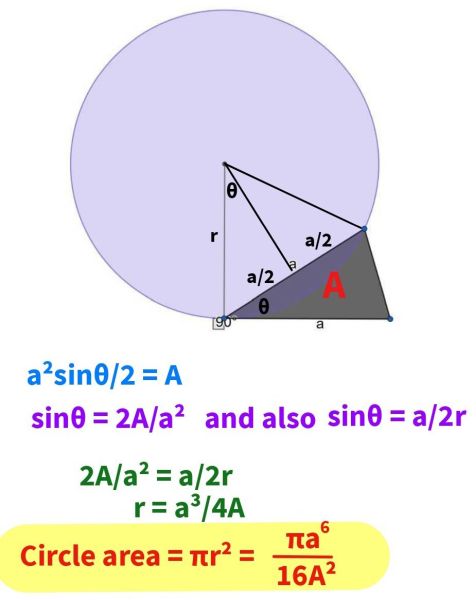
Express the circle area in terms of the isosceles triangle area A and its side length a.
Scroll down for a solution to this problem.
The circle area is πa6/(16A2).
Express the circle area in terms of the isosceles triangle area A and its side length a. https://t.co/2GmEzB84Kv Author: @MarshallWBuck pic.twitter.com/SMPLia1dEO
— Mirangu (@Mirangu1) June 5, 2023
3 replies on “Launch the ball”
The problems seems undetermined (or I a missing something). You can vary the length a of the line segment without changing the size of the circle.
The area needs to be expressed in both a and A.
So your observation is not necessarily a problem, since the change in a can be counterbalanced by that in A to keep the circle constant.
I liked this because I had not seen a 6-th power in an answer before.