A pyramid with a square base and sides that are equilateral triangles contains a cube. If the cube is taking maximum space as shown, what is the fraction of its volume to the pyramid’s volume?

Solution

The volume fraction is 30-21√2, which is approximately 0,30.

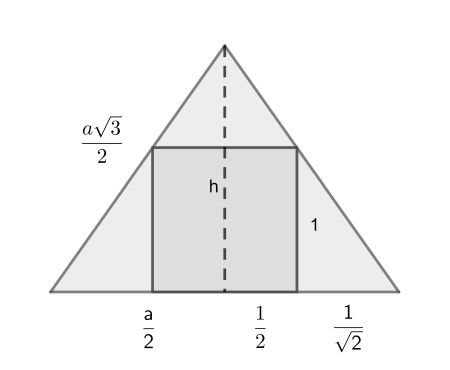
Setting the cube side to 1 for convenience, we have to find the pyramid side a and height h. We can extract this from the cross section shown above. From the Pythagorean theorem in the left side, we derive h=a/√2.

Now going to the right triangle in the lower right corner, which is similar to half the cross section, we can determine its base as 1/√2. This fixes a=1+√2 and h=1+1/√2.

Finally, the cube’s volume is 1 and the pyramid’s is a²h/3, leading to the desired result.