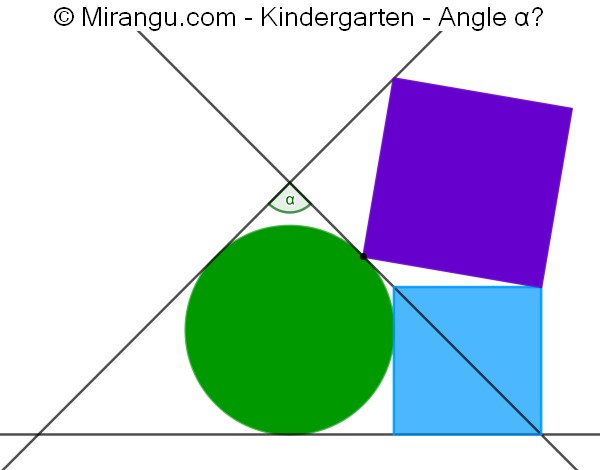
A circle with three tangents and two squares. The accentuated vertex is a tangency point. What’s the angle α?

Solution

The angle α is 90°.

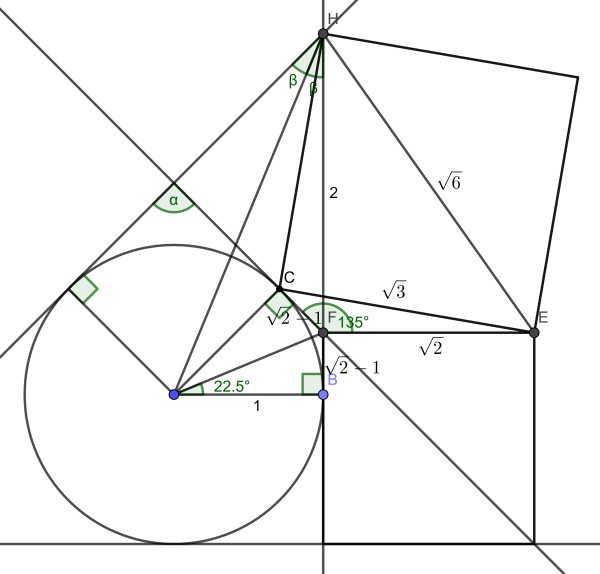
We begin by setting the circle radius to 1 for convenience. Then using an angle chase, the distance BF=tan(22,5)=√2-1. This makes the smaller square of size √2.

Using the cosine rule in triangle CFE then leads to CF=√3. Thus the larger square has diagonal √6. Now the Pythagorean Theorem in right triangle EFH leads to FH=2.

Now tan(β)=1/(√2+1)=√2-1 , leading to β=22,5°. A simple angle chase then leads to angle α=90°.

Poem

Kindergarten
The first year of school
For children aged five
A place where you can stay
A place where you can go
And where you can show what you know
Every day
The child must stay
To help him learn
And help him know
To cherish him and embrace him
And believe in his talent

Bella