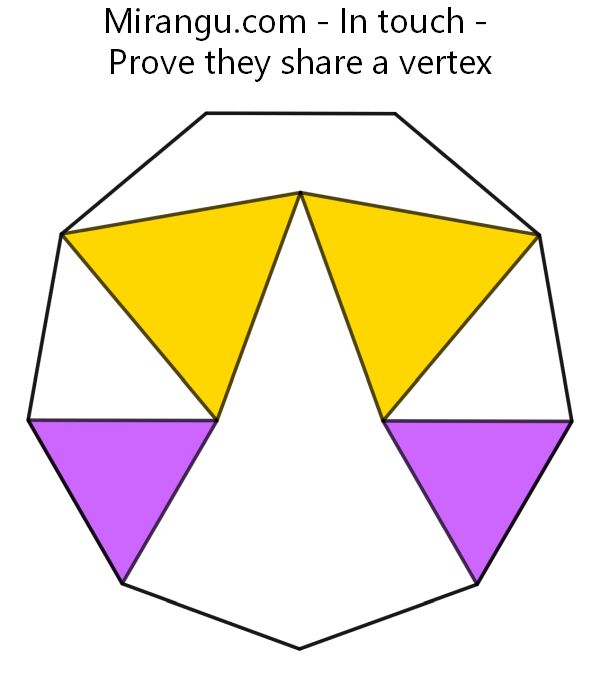
A regular nonagon and four equilateral triangles. The purple and yellow triangles share a vertex. Prove that the yellow triangles also share a vertex.
Scroll down for a solution to this problem.
Solution
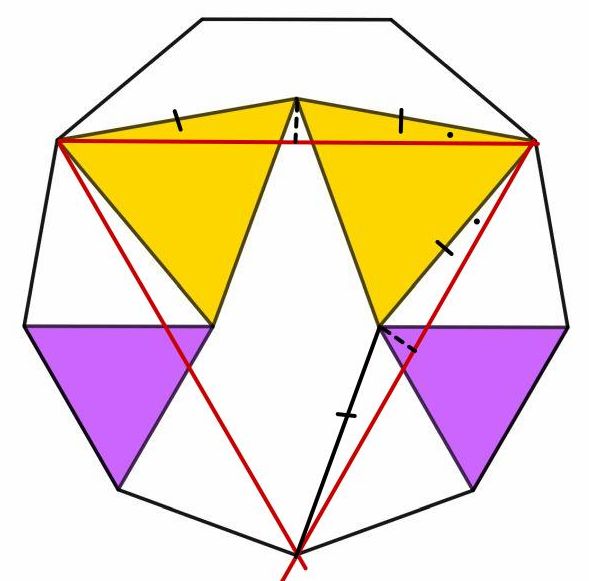
A proof by construction: if the short dashed lines are the same length, then we have two congruent isosceles triangles so the equal sides of the yellow triangle are at 60°. The purple triangles just have to be isosceles for this to work.