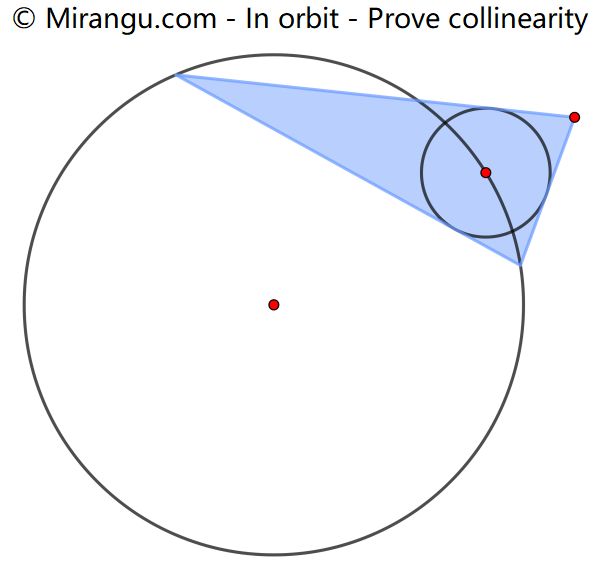
The smaller circle has its centre on the larger circle and is also the triangle’s incircle. Prove that the circle centres and the triangle vertex are collinear.
Scroll down for a solution to this problem.
Solution
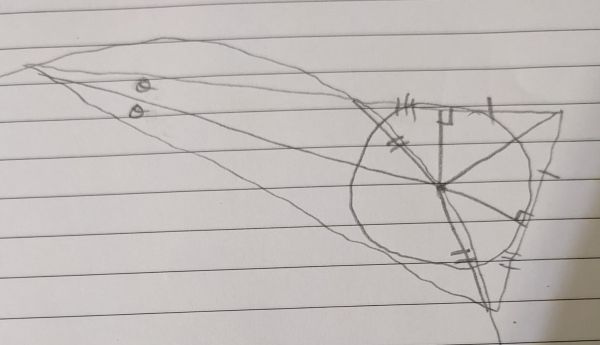
The side lengths of the triangle that are outside the big circle are the same length. Because there are 2 congruent right angled triangles there. For the single hatched lengths, use the Tangent-tangent theorem. For the double hatched lengths, use the fact that equal angles implies equal chords. And for the triple hatched lengths, use RHS congruency.
Poem
In orbit
Moving in space
Floating in a beautiful universe
Piercing gravity
Moon and sun relied together
But in different circles
Sharing the night
The stars
The sky
Dreaming of a big blast
And then come back to earth
For a sunset
So near, so far
To our planet
For which we care