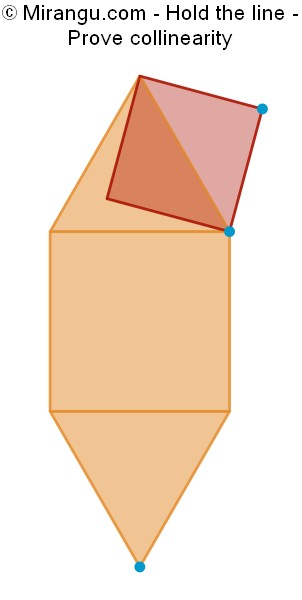
Two squares and two equilateral triangles. Prove the three points are collinear.

Solution

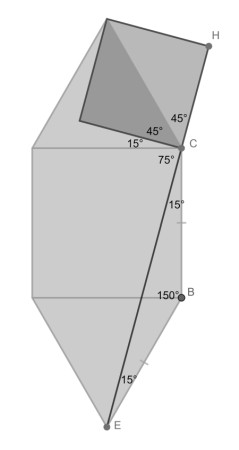
First draw the line segment CE. It is the base of isosceles triangle CEB with top angle 150. The other two angles can found by using the interior angle sum.

Now the angles at point C on the left side of HCE can easily be found. They add up to 180, so HCE must be a straight line.