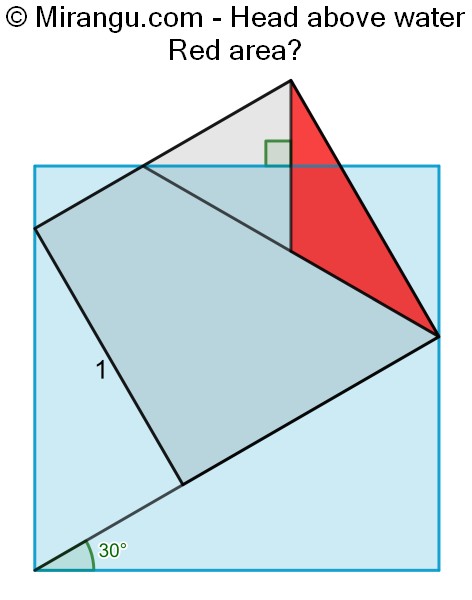
A unit square with an extended side immersed in another square. What is the area of the red triangle?
Scroll down for a solution to this problem.
Solution
The red area is √3/12.
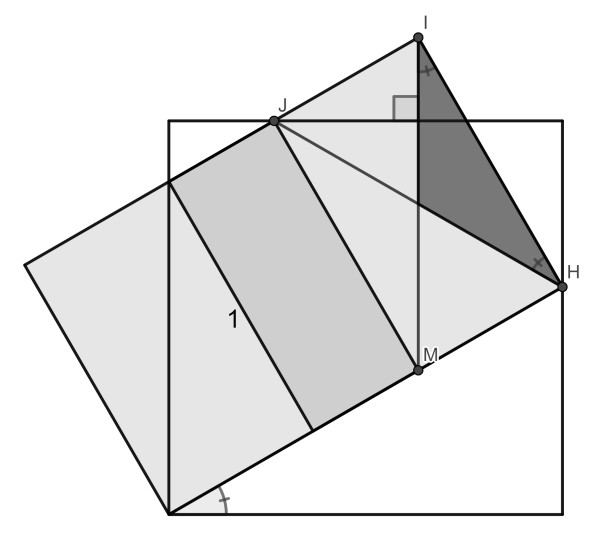
The key is to slide down the tilted square along the extended side such that its vertex coincides with the large square vertex. Since it fitted in horizontally, it will also fit in vertically (90° rotational symmetry).
Now it is clear that MHIJ is a rectangle and moreover the perpendicular line segment extends to its diagonal MI. The other diagonal HJ was already drawn. Clearly, the red triangle is isosceles with its congruent angles equal to the tilt angle 30°. Its area is easily calculated as tan(30°)/4.
Poem
Head above water
The square controls the tide
In deep water
May be coming from rain clouds
It’s a fresh breath coming out
Just as a secret of my mouth
No muddy water
Everything fresh and clear
My thoughts swim without any fear
For all the souls
Far and near