The vertices of an equilateral triangle are connected to an interior point. What is the angle α?

Solution

The angle α is 45°.

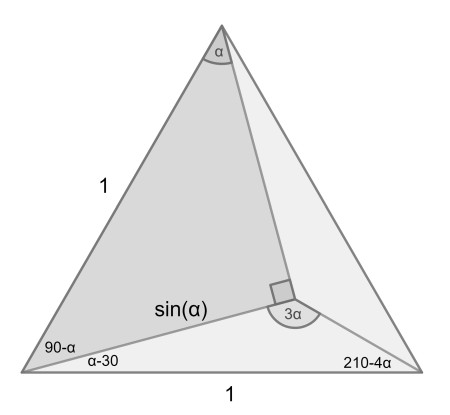
Some elementary angle chasing gives the above. Now we can apply the Law of sines in the bottom triangle: sin(α)sin(3α)=sin(210-4α). This can be rewritten using trigonometric rules as (cos(2α)-cos(4α))/2=sin(4α)√3/2-cos(4α)/2, which simplifies to cos(2α)=sin(4α)√3=cos(2α)sin(2α)2√3.

So, either cos(2α)=0 or sin(2α)=√3/6. The latter solution does not give an interior meeting point. The former amounts to α=45°.

Poem

The glass pyramid
A sublime monument
From ancient times
Shines like a diamond
Amidst the neon lights
A pyramid of glass, metal or stone
The moon is reflected
In its glittering façades
And its countless steps
Gigantic stairway for the soul
To ascend to heaven
The final goal

Bella