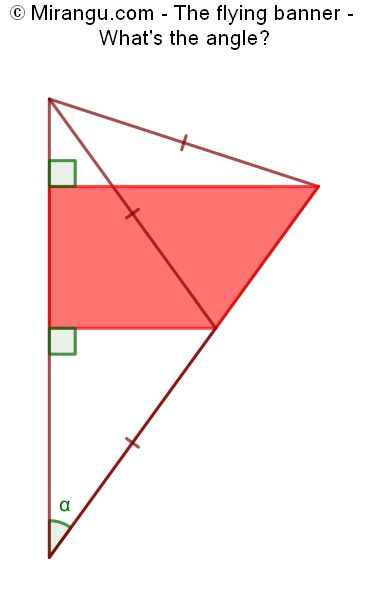
A triangle with a quadrilateral that covers half its area. What is the angle?
Scroll down for a solution to this problem.
Solution
The angle is 36°.
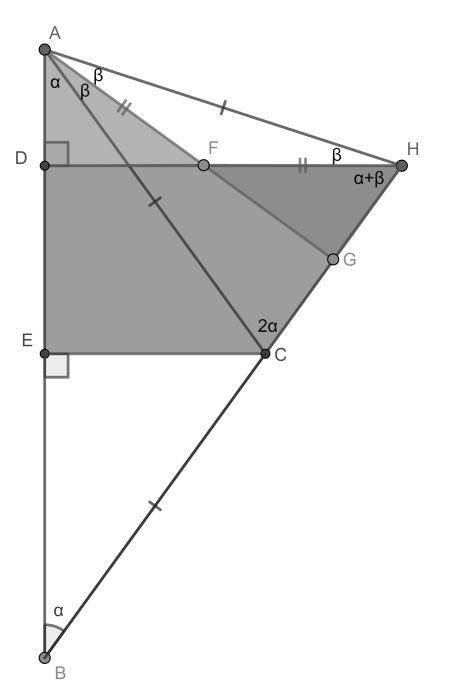
First, recognise that the triangle consists of two isosceles triangles BCA and CAH. These are divided in half by altitudes from the top angles CE and AG respectively.
Now consider triangles ADF and HGF. They are similar from comparing angles. But from the area constraint it also follows that they have equal area. Therefore they are congruent.
This makes AFH isosceles and by looking at angles BAH also becomes isosceles. Now the angles can be filled in as shown, and since β=90-2α it follows that 180-3α=2α. This gives α=36°.
Please take a look at the Desmos calculator of The flying banner made by Per Henrik Christiansen. You can play around with the parameters to see how that affects for instance the area fraction of the red quadrilateral.
Poem
I’m may be just a kite
I’m the king of the air
I fly to get free
I leave my soul and spirit
In the sky
Just flying for fun and get high
Flying for liberty
Making love with the wind,
the clouds,
It’s like music playing on my wings
I’m happy
I smell
I fly