A right triangle with its inscribed circle. Two cevians are drawn through the circle centre. What is the circle area in terms of triangle areas A and B?
Scroll down for a solution to this problem.
Solution
The circle area is 2πAB/(A+B).
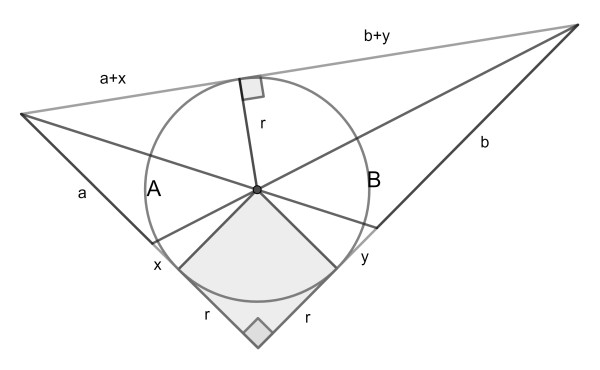
First note that the two triangles both have height r, which is also the circle radius. Name their respective bases a and b. The two little triangles have bases x and y.
From triangle similarity one can show that x/r=r/(b+y) and y/r=r/(a+x). Eliminating r from these two equations leads to x/y=a/b. So we get that b+y=(a+x)b/a=bz/a, where we temporarily named a+x=z. Filling this back in we get that r2=yz=xbz/a.
Now the total area is (r+z)(r+bz/a)/2. By adding up the area of the square and the four right triangles we get that this must be equal to r2+rz+rzb/a. After some algebra, also using the equation for r2, we get xb/a+r+rb/a-bz/a=0. Eliminating z, this leads to r=ab/(a+b).
Finally, using A=ar/2 and B=br/2, we reach the desired formula.
Poem
The eye mask
It’s a nice blindfold
And covers the eyes
It’s good for air travel
And shut out light
It’s used for weight lifting
Or for hostage kidnapping
And in magic tricks performing
Many other activities use blindfolding
It’s a powerfull symbol
In a form of awakening

One reply on “The eye mask”
Another approach is to express A , B, and r as functions of the two side lengths, say a and b (not the usage in the Solution above), and then show that the combination 2AB/(A+B) agrees with r^2.
First, for right triangles, we have the easy formula for the radius r of the incircle: 2r = a+b – c, where c=sqrt(a^2+b^2) is the length of the hypotenuse.
Second, angle bisectors split the far side in the same ratio as the other two side lengths. The A and B triangles have heights r and bases given by that ratio property:
base_A = (c/(b+c))*a
base_B = (c/(a+c))*b
Thus
A = base_A*(r/2) = (c/(b+c))*a*(a+b-c)/4,
B = base_B*(r/2) = (c/(a+c))*b*(a+b-c)/4.
AB = c^2 a b (a+b-c)^2 / (16( b+c)(a+c))
A+B= c (a+b-c) {a/(b+c) + b/(a+c)}
= c (a+b-c) (a^2+b^2 + (a+b)c)/(4(a+c)(b+c))
4AB/(A+B) = cab (a+b-c) / (a^2+b^2 + (a+b)c)
= cab (a+b-c) / (c^2 + (a+b)c)
= ab (a+b-c) / (a+b+c)
= ab (a+b-c) ^2/ ((a+b+c)(a+b-c))
= ab (a+b-c) ^2/ ((a+b)^2-c^2)
= ab (a+b-c) ^2/ (2ab)
= (a+b-c)^2/2 = 2*r^2.