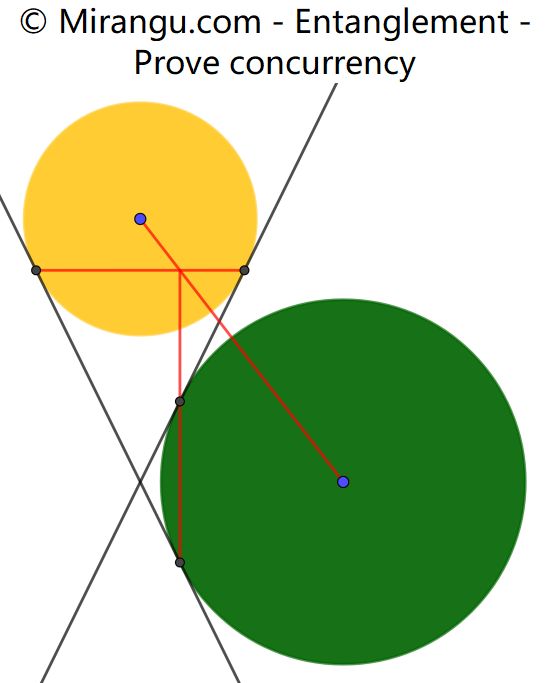
Two circles with two common tangents. Three red lines through tangency points and centres. Prove that they are concurrent.
Scroll down for a solution to this problem.
Solution
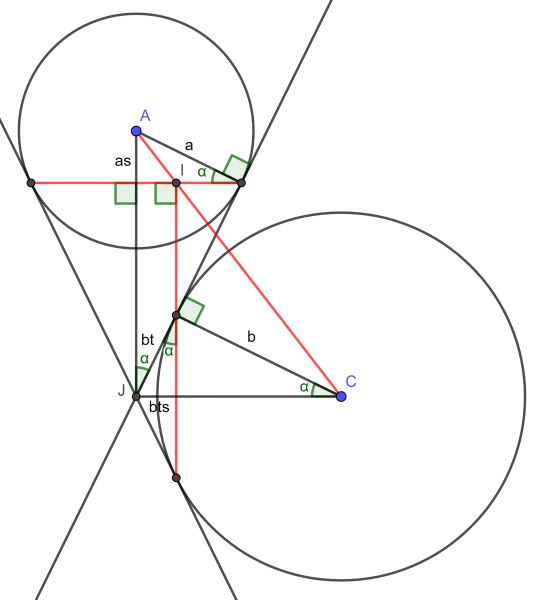
This solution starts by establishing point I as the intersection of the two lines through the tangency points. By carefully finding angles as shown in the diagram above, tan(∠JAC) is easily found as (b/cos(α))/(a/sin(α))=btan(α)/a. A bit more elaborate is tan(∠JAI), which works out to (btan(α)sin(α))/(asin(α))=btan(α)/a. Therefore ∠JAC=∠JAI and hence I is the common intersection point of the three red lines.
Poem
Entanglement
A maze of branches and twigs
Tangled up in a yellow sun
The roots grow skywards
Azure blue
The antler is eternal
Nourished by light
It grows and prospers
A superposition of colours
Inspiration of hope
Lit by an orange sun