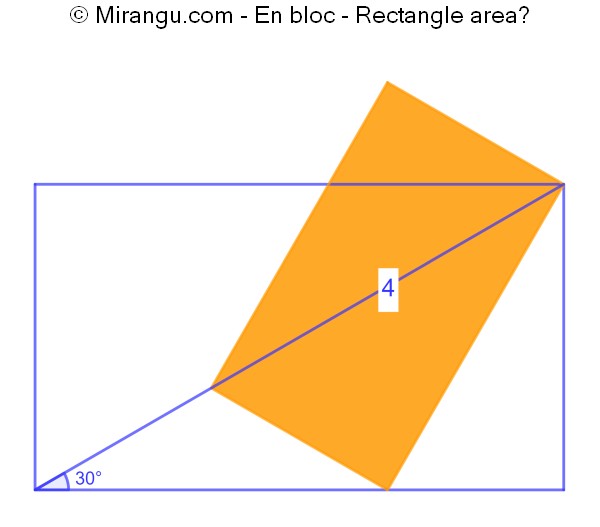
Two similar rectangles. If the small one has area 4 what is the area of the large rectangle?
Scroll down for a solution to this problem.
Solution
The large rectangle has area 9.
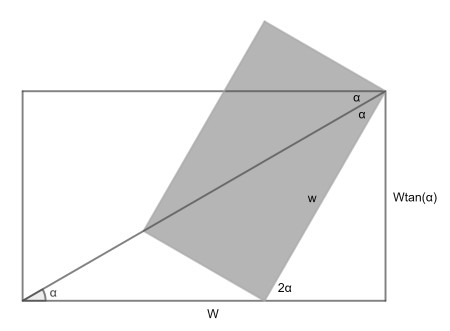
We will find the solution for a general angle α. Calling the large width W, its height will be Wtan(α). Now, from parallel lines and the similarity of the rectangles, we can fill in the other angles as shown.
In the 2α right triangle, the hypotenuse w=Wtan(α)/sin(2α)=W/(2cos2(α)). Hence W/w=2cos2(α). Because of similarity, the proportion large rectangle area : small rectangle area is the square of that: 4cos4(α).
Poem
An orange rectangle is hiding
From figures who want
To know him
He is shy, and lonely feeling
Wants to have friends and outside going
Only with love and not discriminating
From circles, squares or triangles threatening
He is not complaining
Just so many feelings overwhelming