Four circles share one point. The quadrilateral has vertices which are intersections of pairs of circles, and three of its coloured edges are tangent to the circle of the same colour. Show that the fourth edge is also tangent to its circle.
Scroll down for a solution to this problem.
Solution
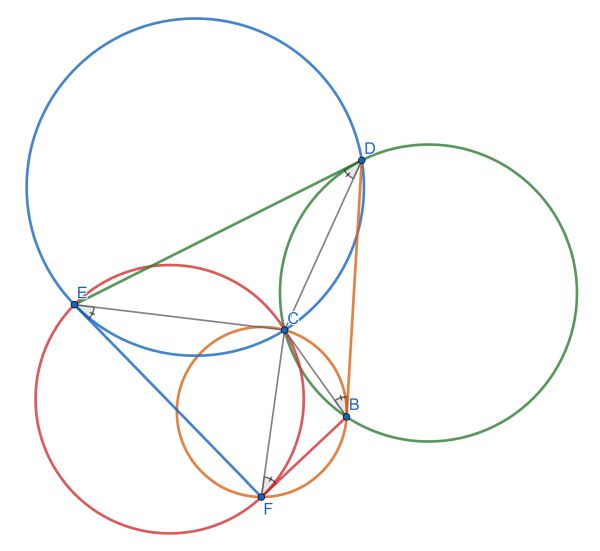
The reasoning is as follows: suppose green, orange and red are tangent. Using the alternate segment theorem, green implies ∠EDC=∠DBC, orange implies ∠DBC=∠BFC and red implies ∠BFC=∠FEC. So ∠FEC=∠EDC. Then the reverse of the alternate segment theorem implies that blue is also tangent.
One reply on “Cycling of tangents”
I could have used any number of circles. The diagram was getting complicated with 4 and I probably would have done three instead but Rik figured out how to remove lines and other decorations by using colors cleverly.