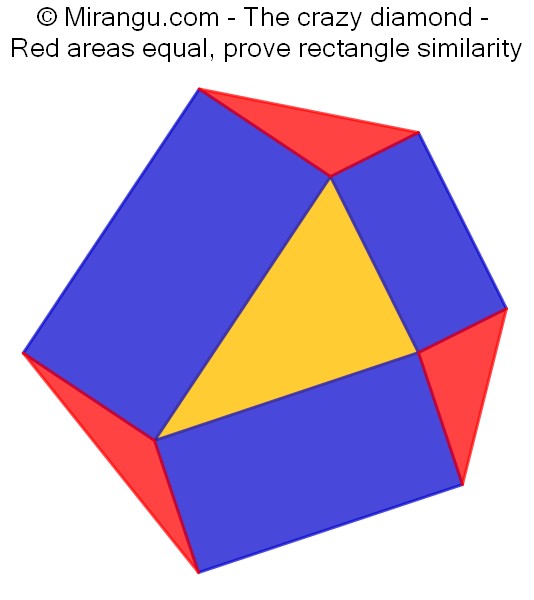
Three rectangles and four triangles. Given that the red triangles have equal area, prove that the blue rectangles are similar.
Scroll down for a solution to this problem.
Solution
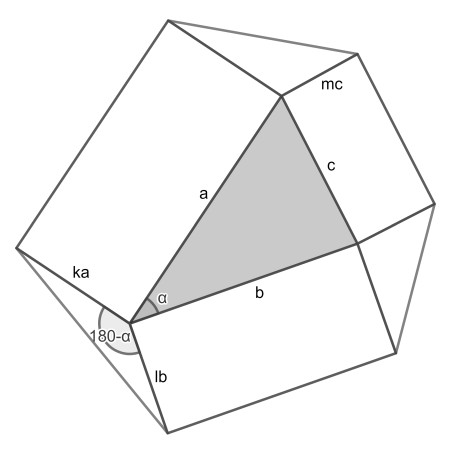
Naming the sides of the rectangles as shown. Now the lower red triangle has area k*l*a*b*sin(180-α)/2, whereas the central yellow triangle has area a*b*sin(α)/2. It is not hard then to show that red is k*l*yellow. Likewise the other red triangles are l*m*yellow and k*m*yellow.
Since they are given to be equal, we have k*l=l*m=k*m, which can be simplified to k=l=m. This implies similarity of the three rectangles.
Poem
The crazy diamond
He’s like glass or made of crystal
He’s unique, a jewel
Cut of the mountains
Out of the stones
So brightly clear
So beautiful, so dear
But the nicest diamond is life
probably
Using the day and time surely
The life is
As precious as gold
A gift to hold !