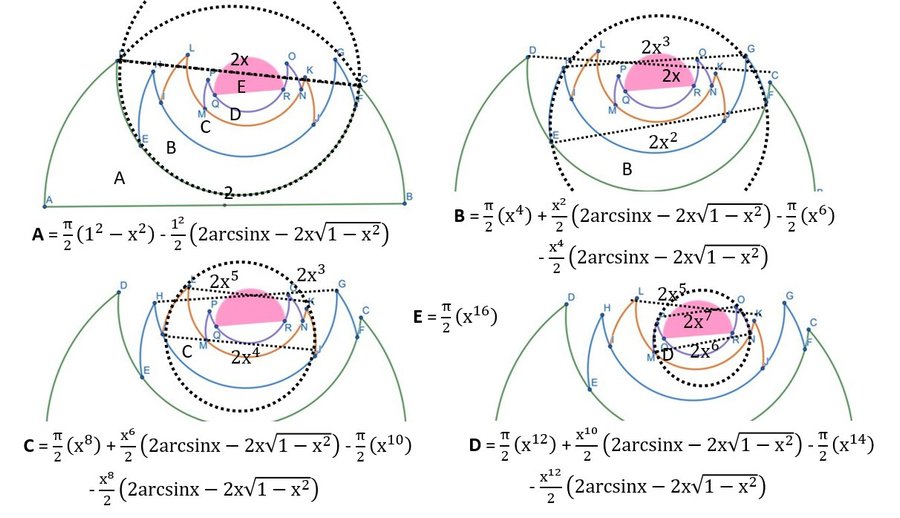
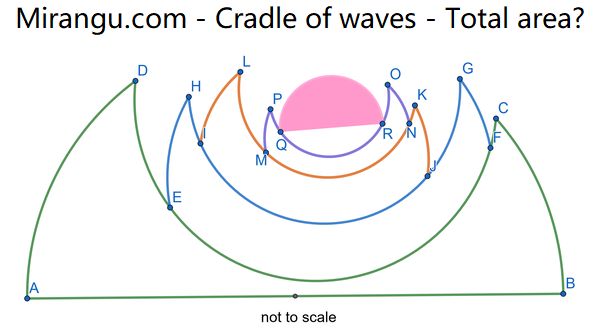
What is the area of the entire figure (in terms of x) given that the segments AB, CD, EF,…, QR are all semicircle diameters, and the lengths decrease geometrically ( AB=2, CD = 2x, EF= 2x^2, GH = 2x^3,…)?
Scroll down for a solution to this problem.
What is the area of the entire figure (in terms of x) given that the segments AB, CD, EF,…, QR are all semicircle diameters, and the lengths decrease geometrically ( AB=2, CD = 2x, EF= 2x^2, GH = 2x^3,…)? https://t.co/BxdV2t8447 By @MarshallWBuck pic.twitter.com/DjQURHEYtW
— Mirangu (@Mirangu1) April 26, 2024
One reply on “Cradle of waves”
I counted the area between the pink half-circle and the waves.
Also, I added everything up in the finite geometric series, using the fact that (1-x^2+ x^4-…-x^14) = (1-x^16)/(1+x^2).
I defined c = pi*x^2/2 + arcsin(x) – x*sqrt(1-x^2), which is the area of an “egg-like figure” bounded on one side by a circular arc of radius 1 and on the other side by a semicircle of radius x. Then the full area (that I intended, including the space between the pink semicircle and the wave) is the area of the biggest semicircle, pi/2, minus the egg with area c, plus the egg with area c*x^2, minus the egg with area c*x^4, etc, and finally plus the final egg c*x^14. The final answer is
pi/2 – c*(1-x^16)/(1+x^2).