A triangle with a cevian. What’s α?
Scroll down for a solution to this problem.
Solution
α is 15°.
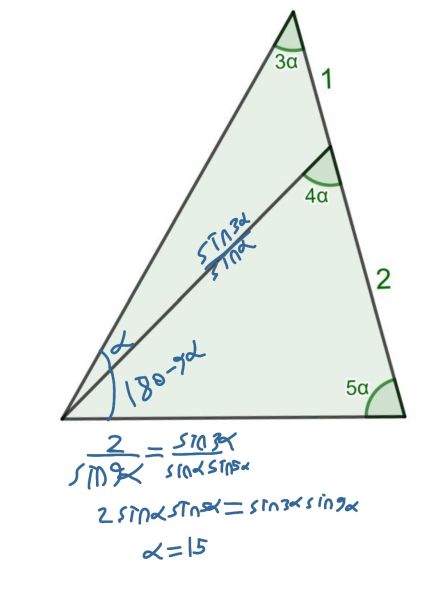
It must be said that there are more solutions to the equation, but then 5α exceeds 180°, which is not allowed.
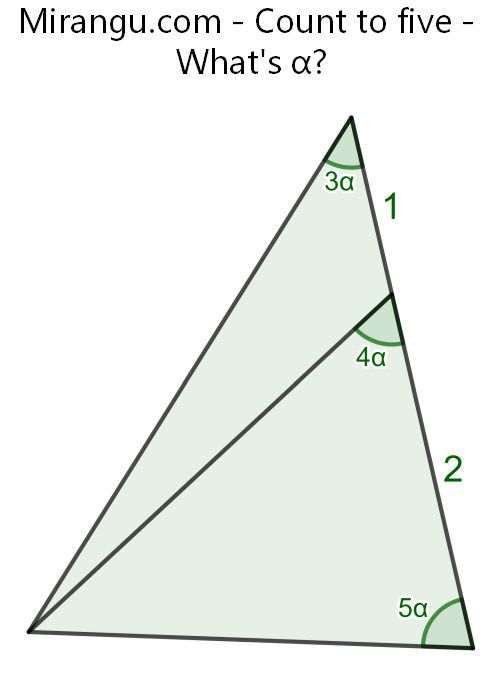
A triangle with a cevian. What’s α?
Scroll down for a solution to this problem.
α is 15°.

It must be said that there are more solutions to the equation, but then 5α exceeds 180°, which is not allowed.
A triangle with a cevian. What’s α? https://t.co/zbR94dBg6H Inspired by Di Pasquale ea. pic.twitter.com/BJbwRk1moM
— Mirangu (@Mirangu1) February 24, 2023
2 replies on “Count to five”
2sin(a)sin(5a)=sin(3a)sin(9a) can be ‘solved’ by verifying it holds for a ‘lucky’ guess of a=15. How else can the answer be found?
Reply to Lewis Corner comment:
Maybe not so satisfying, but it is possible to expand the equation using trig identities (various angle sum formulas …), obtaining a polynomial equation in sin(α), or in cos(α). It turns out this eq. can be expanded as a polynomial in cos(2α).
Let u = cos(2α). Then the above eq. is equiv. to a 6th degree polynomial in u. And that polynomial factors as:
(u – 1)(4u² – 3)[ 2u(2u + 1)² – 1] = 0
The first two factors give non-neg sol’s u = 1, u = √3/2 and not hard to show the 3rd factor gives a non-neg solution that is less than 1/2.
Since u = cos(2α), these three solutions for u yield the following values of α that are between 0 and 90 degrees:
α = 0°, α = 15° and a > 30°.
We want α > 0 and since the figure has a triangle that has angle sum greater than 9α, we need α < 20°. Of the three values found from the polynomial eq, only α = 15° works.
———————————————
I agree that it would nice to see this obtained from a geometrical solution that avoids the use of trigonometry. Still thinking about whether that can be done…