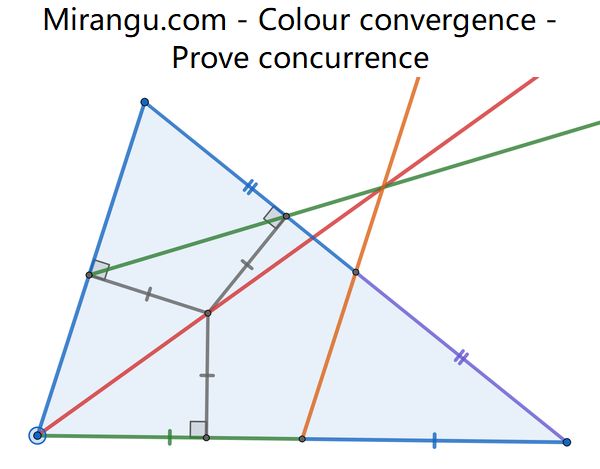
A green line connects two points of tangency of a triangle to its incircle. A red line is the angle bisector at a vertex, and an orange line connects the midpoints of two sides. Show that the three lines are concurrent.
Scroll down for a solution to this problem.
Solution
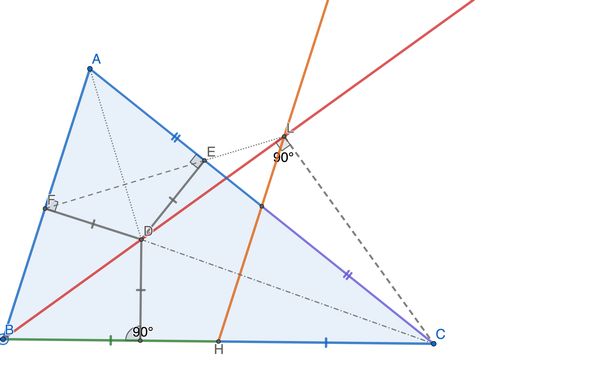
L is defined as the intersection of the red and orange lines, and we intend to show that F, E, and L line up. Note that HL = BH (because angle DBH = angle DBA = angle BLH, this last using LH || AB.). This implies BLC is a right angle, and thus DELC is a cyclic quadrilateral (having two right angles in it). That implies the angles LEC = LDC = B/2 + C/2. Meanwhile, angle AEF is 90 – A/2 = B/2 + C/2. So FEL is a straight line.