Two semicircles are tangent to each other’s diameter. Are the line segments connecting their corners parallel?
Scroll down for a solution to this problem.
Solution
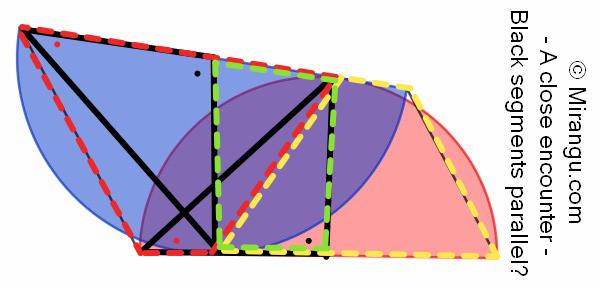
The green vertices are the tangency points and the circle centres, with right angles at the tangency points and supplementary angles at the circle centres. The red and yellow quads have vertices at the diameter ends and tangency points.
The three dashed quads are all cyclic – green has two opposite right angles, so the angles marked black are equal, so the ones marked red are also equal (isosceles triangles); so the red quad is cyclic & similarly for yellow.
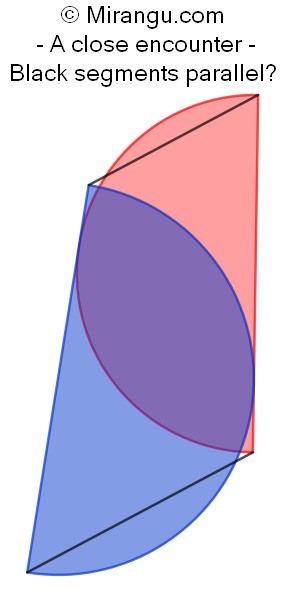
One reply on “A close encounter”
Trivial if diameters are parallel. Otherwise all semicircles are homothetic with respect to the distant intersection of extended diameters. Therefore the ratio of distances of diameter ends to that far intersection point are all the same, independent of locations of the semicircles. This implies that the diameter ends connect by parallel lines.