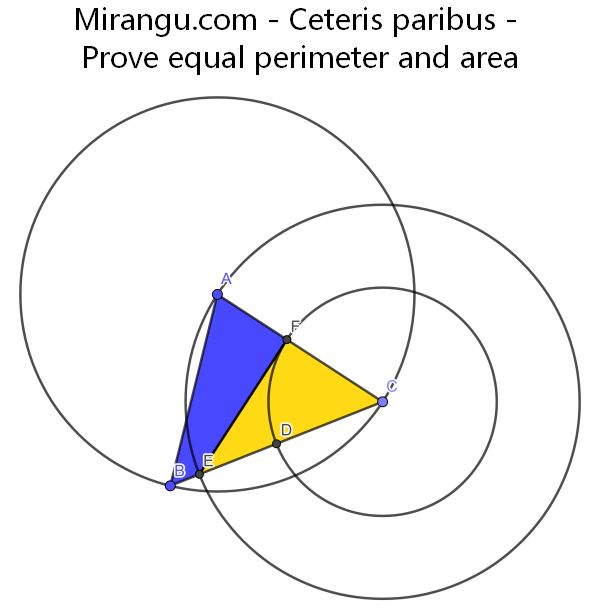
Three circles with their centres and a triangle ABC. Given that D is the midpoint of BC, prove that quadrilateral ABEF and triangle ECF have both equal perimeter and equal area.
Scroll down for a solution to this problem.
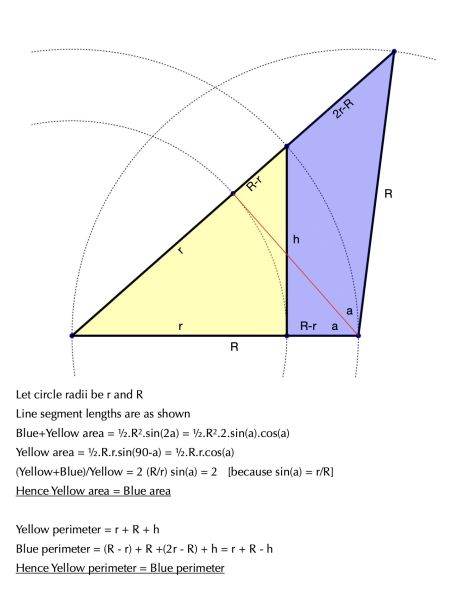
Solution
Poem
Ceteris paribus
“All things being equal”
But it’s not so easy
Things are changing
Around us and in life
Our choices
And our mistakes
What is constant and equal
Is our changing
Even if we try to do the best