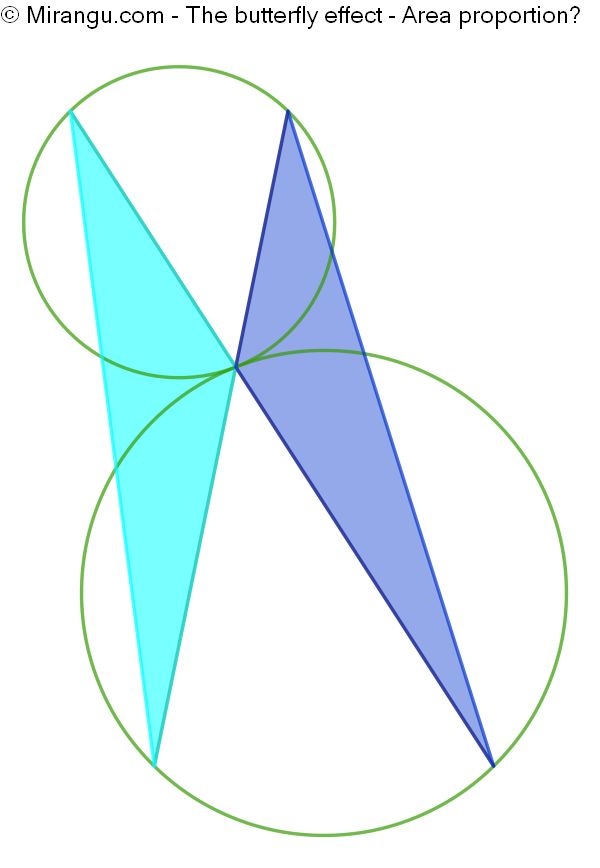
Two touching circles and two lines passing through the tangency point. What is the area proportion of the two triangles?
Scroll down for a solution to this problem.
Solution
The area proportion is 1, because both triangles have equal area.
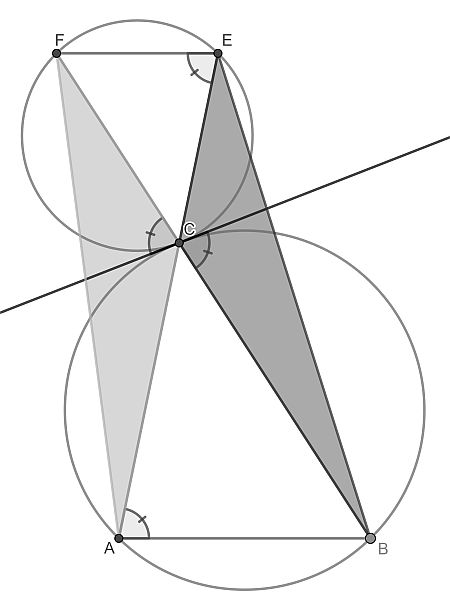
We thank Rony Sarker and Asmit Dey for this elegant solution.
The first part of the solution is to proof that line segments AB and EF are parallel. This can be done by propagating angle BAC upwards.
- Angle BAC equals the angle of line BC and the tangent due to the tangent-chord theorem.
- This angle equals the one on the other side of the crossing lines.
- That angle equals angle CEF again due to the tangent-chord theorem.
Now if a transversal line cuts two lines at equal angles, these lines are parallel.
Because they have the same base and height, triangles ABE and ABF have the same area. Subtracting their overlap ABC therefore also leaves two equal areas.
Poem
The butterfly is learning every day
How to fly away
He comes from a small chrysalis
Wanting to grow, evolving a New butterfly to go
Webbing his silk heart
Drinking the flowers nectar
Or just like a lovesick letter
Brought to love better
He’s cuddling your eyes and your skin.