Two overlapping regular pentagons share two vertices. What fraction is the overlap area?
Scroll down for a solution to this problem.
Solution
The gold fraction is 1/(5φ+4), which is approximately 8,27%.
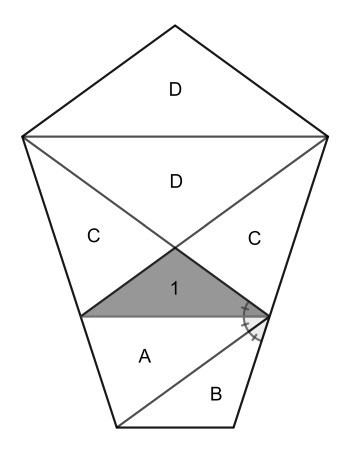
The basic knowledge needed is that a regular pentagon’s diagonal length is φ times its side length, where φ is the Golden Ratio. Scaling such that the gold area is 1, and using also the fact that the diagonals trisect the corners, we easily find that A=φ and B=1.
From triangle similarity and comparing the bases, we find that D=φ2=φ+1. Since C+1=D, we get that C=φ. Adding it all up, we find for the total area 5φ+4.
Poem
The bishop wears a mitra
He must not be a clown
Wearing red shoes and crown!
He is well known
To confirm us in Rome
His beautiful mitra
Makes a triangle
Fantastic and extra !
Grandiose decorations
He blesses for reconciliation
With his beautiful crown
Just not to be unknown

