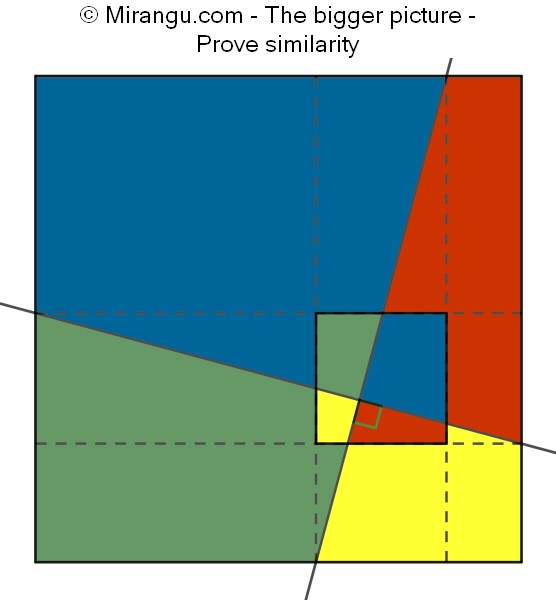
In a small square two perpendicular lines are drawn. A larger parallel square is constructed as shown. Prove it is a scaled copy of the smaller square but rotated 90° anticlockwise.

Solution

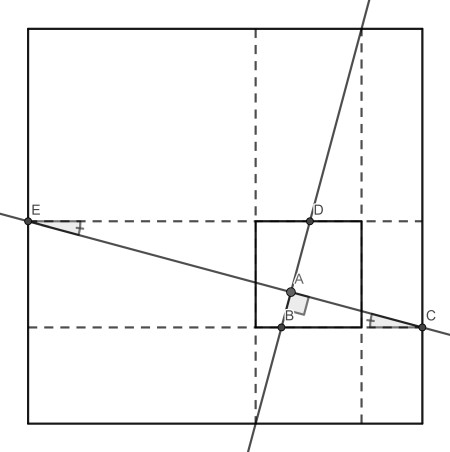
First, since the squares are parallel, the angle α of the perpendicular lines with the side (angle AED) is the same. It is not hard to show that the square scaling factor is actually tan(α).

Now consider the similar right triangles ABC and ADE. They give AD/AB=AE/AC. In other words, the intersection point A is in the small square vertically at the same position is it is in the big square horizontally.

This can be proved equally for the small horizontal and big vertical direction. Combined with the same slant angle α, this proves the square similarity.