The edges of a cyclic quadrilateral extend to two intersections. O is the circle centre. The two diagonals intersect inside the circle. What is the angle α?
Scroll down for a solution to this problem.
Solution
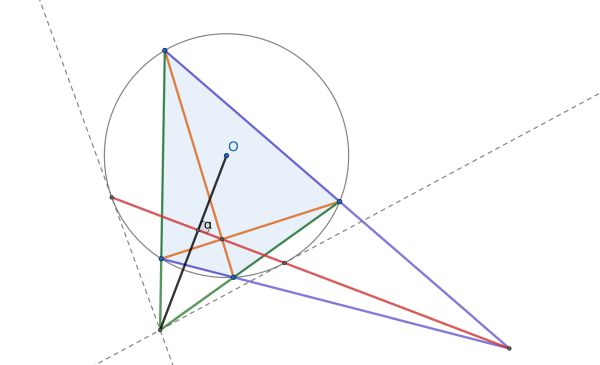
This is easy if you know this standard way to construct the tangents from an external point to a circle: Suppose the external point P is the intersection of the green sides of the cyclic quadrilateral. Then, to find the points of tangency, one takes any two lines through P intersecting the circle in four points (take say the two green lines!), find the intersection points of the diagonals and the other sides (the orange and purple lines), form the red line connecting them, and then intersect the red line with the circle to find the desired points of tangency.
Then, of course, alpha is 90 degrees, because the radial line from the circle center O to P is perpendicular to the chord connecting the points of tangency.
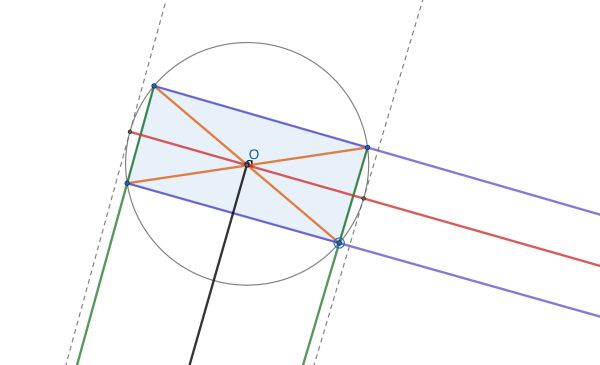
The easiest way I know to show that the construction works is one that requires knowing just a little bit of projective geometry. There will be a projective transformation that sends the circle into itself but moves the intersection of the orange diagonals to the center O of the circle. Then the new green lines must be parallel, the new purple lines must be parallel to each other but perpendicular to the green lines, the red line will be a diameter halfway between the two purple lines, and the tangents from P (now at infinity) to the circle will be parallel to the green lines and touch the circle where the red diameter intersects it.
Challenge
We urge the reader to come up in the comments with a solution that does not use polars but is purely Euclidean or trigonometric.
One reply on “Baby steps”
No solution as challenged – so I send a 2nd way although polars are used.