Three discs have one 3-way common point on their boundaries. Where do the red rays intersect? How are the points of intersection related to the common boundary point?
When worlds collide
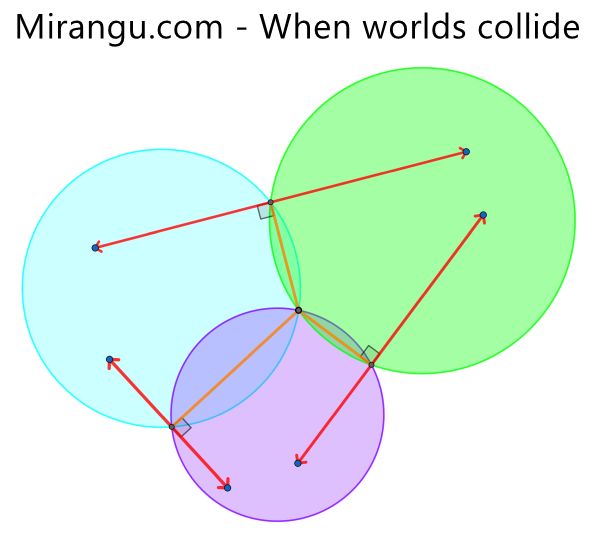

Three discs have one 3-way common point on their boundaries. Where do the red rays intersect? How are the points of intersection related to the common boundary point?
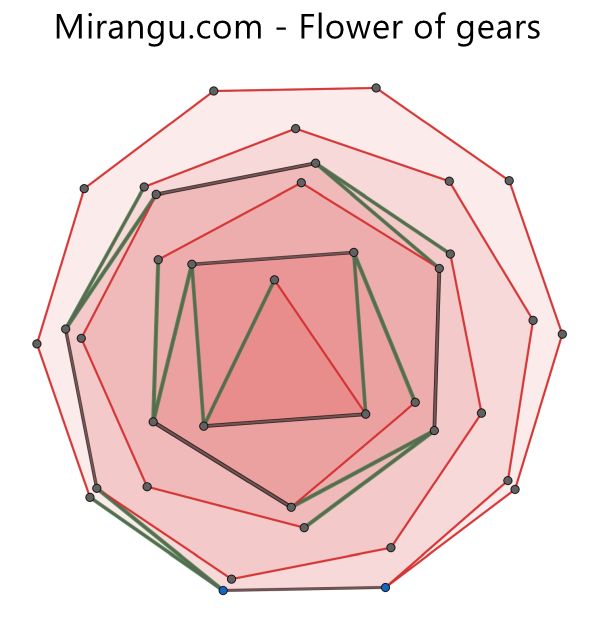
During one step every internal polygon rotates to the next position along its outer polygon, merging two green sides. How many full turns are made by the innermost triangle before the entire configuration returns to its initial state?

The left wall of a rectangular pit can slide frictionlessly along the floor. An inward force of F is needed to maintain the position of the 6 congruent circles, but a larger force G is needed to push the walls inward, lifting the circles. What is G/F?
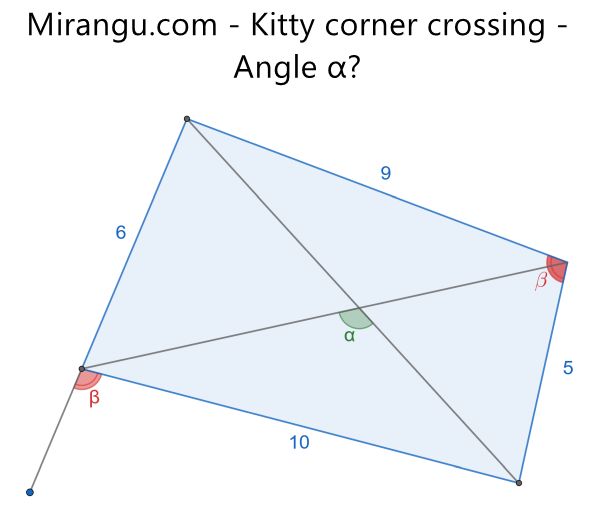
What is the green angle α between the cross ways?

Orange and Blue disks have a common tangent line IK intersecting DB at A. The red circle has chord DB, and tangents AF and AG. Show that the chord FG , the line DB, and two of the common tangents (LM and OP) have H in common.
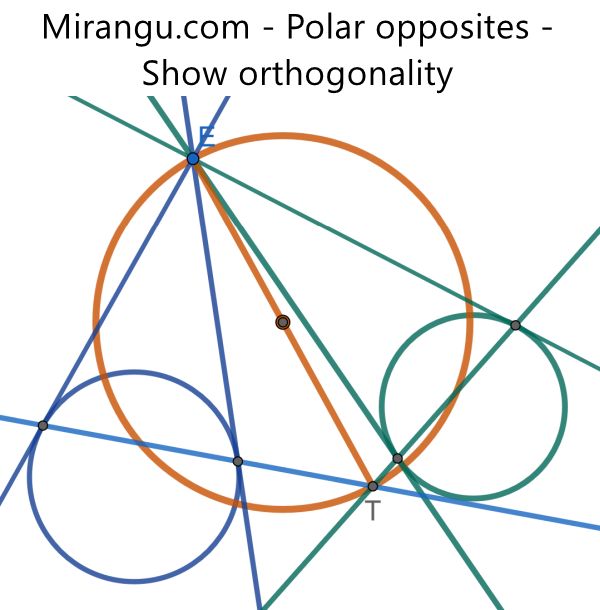
The polar lines for a point E with respect to the blue and green circles intersect at a point T. Show that the orange circle with diameter ET intersects the other circles orthogonally.
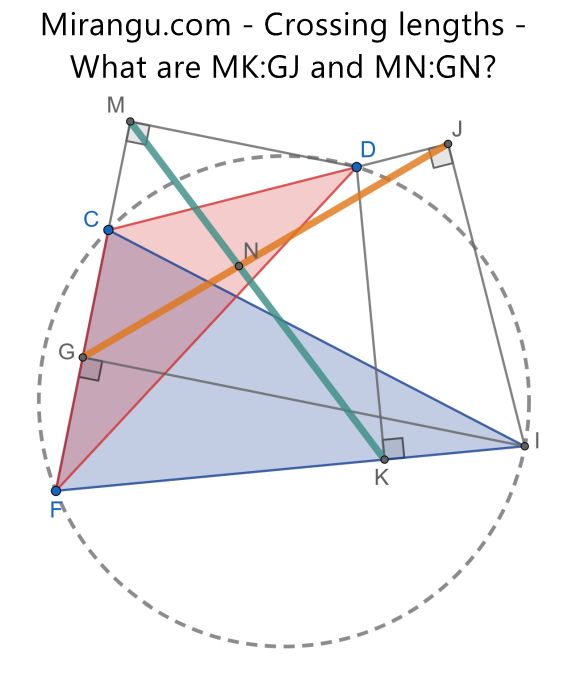
A cyclic quadrilateral (CDIF), where we form two segments: MK (green) with DM perp to FC and DK perp to FI; GJ (orange), with IG perp to FC and IJ perp to CD. What is the ratio MK:GJ ? What about MN:GN?

A circle of radius r is interior-tangent to the larger yellow circle of radius R, with diameters overlapping. Express s/k in terms of r and R.
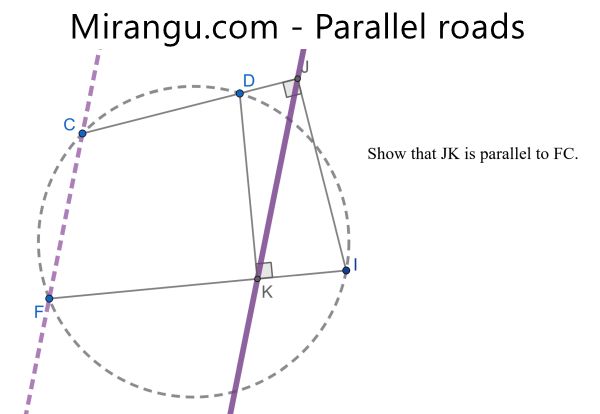
The cyclic quadrilateral FCDI, with points K such that DK perp to FI and J such than IJ perp to CD. Show that JK is parallel to FC.
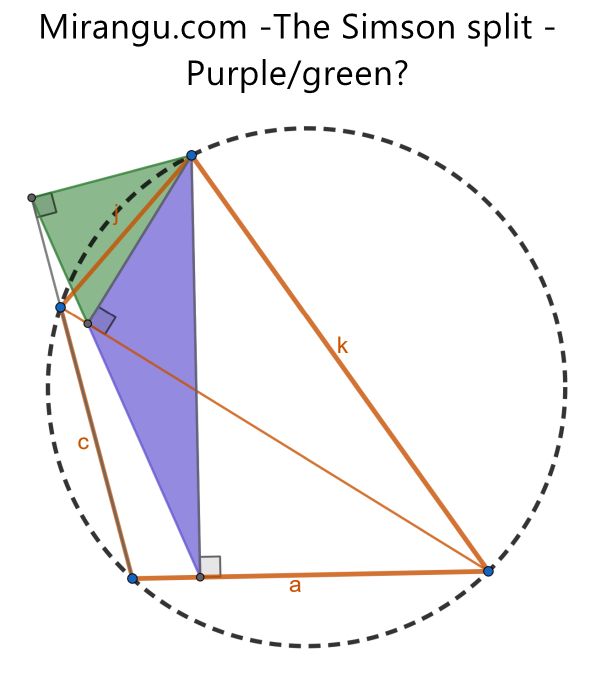
A cyclic quadrilateral has side lengths a, c, j, and k. Three segments drop perpendicularly to two sides and one diagonal of the quad, forming the green and purple triangles between them. What is the ratio purple/green, in terms of a, c, j, k?
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now