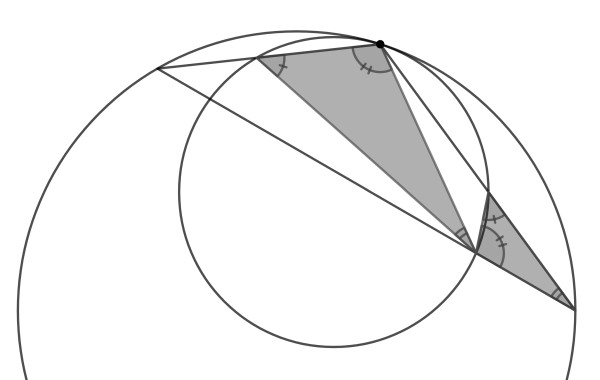
A semicircle and a circle are tangent. The tangency point is shown. Prove that the two coloured triangles are similar.
Scroll down for a solution to this problem.
Solution
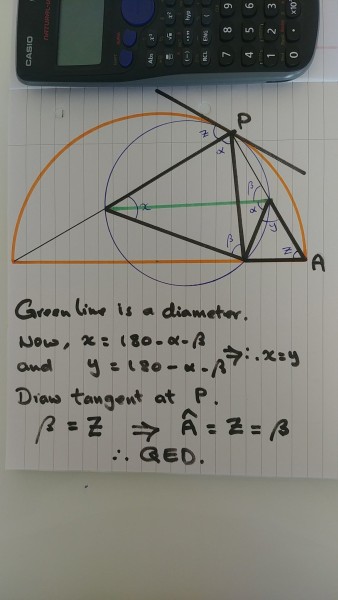
Note that this solution never uses the right angle at P. The prove therefore is also valid for non-diameter chords.
Poem
As within so without
With a triangle in interactions
And power and responsability in connection
In this triangulation
Each one has a singular position
People seem not able to take decisions
In Karpmann’s triangle, it’s difficult to analyse
And to know well the motivations

One reply on “As within, so without”
Absolutely so.
At first I was going to make use of the diameter. But when I labeled alpha and beta, I realized that I didn’t have to after all. Thanks for bringing the generality of it to my attention as it had not occurred to me.