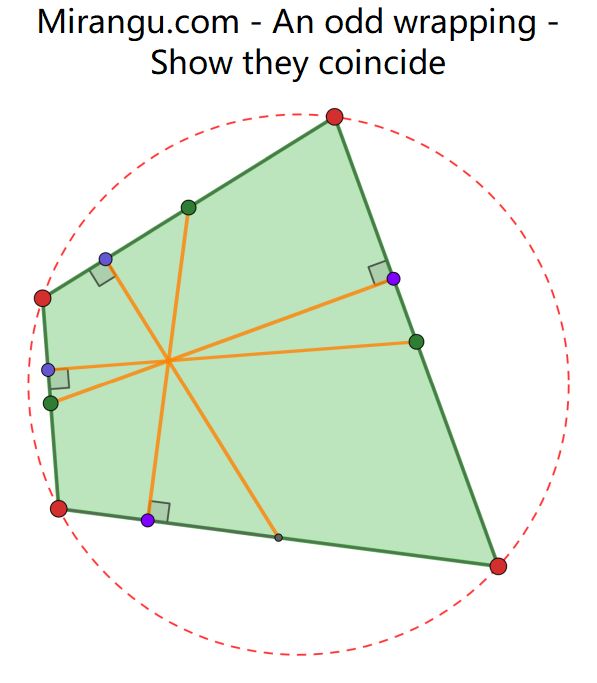
A present fits inside a circle, and we tape the orange ribbons to the green midpoints of the sides, choosing them perpendicular to the opposite sides at the purple points. Show that the four ribbons have a point in common.
Scroll down for a solution to this problem.
Solution
If the circle is centred at 0, the vertices of the cyclic quadrilateral are the vectors A, B, C and D, all of the same length. The common point is E=(A+B+C+D)/2. Then (E – (A+B)/2) = (C+D)/2, which is perpendicular to D-C because C and D have the same length.
One reply on “An odd wrapping”
A 2nd way to the ‘anticenter’ E