A triangle divided by three line segments. What fraction is blue?
Scroll down for a solution to this problem.
Solution
The blue fraction is 2/7.
Categories
An irregular tiling
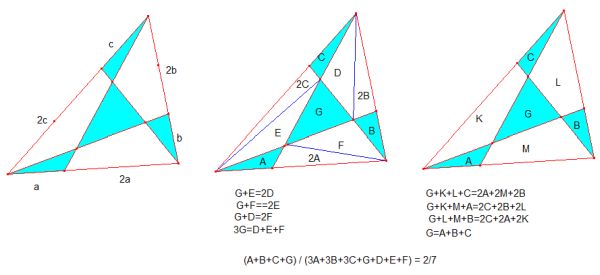
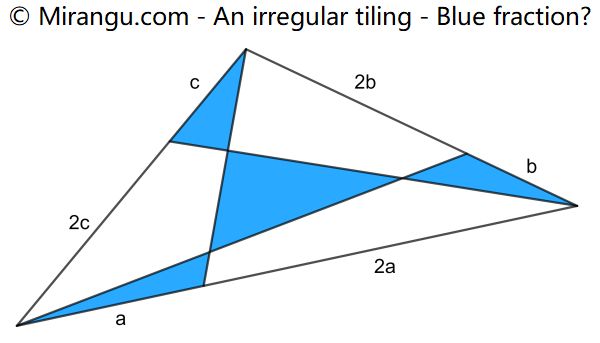
A triangle divided by three line segments. What fraction is blue?
Scroll down for a solution to this problem.
The blue fraction is 2/7.
6 replies on “An irregular tiling”
Solution with ROUTH’s Theorem
If an interior triangle has vertices given by barycentric coordinates
(a,b,c), (d,e,f), (g,h,i), then the fraction of the whole triangle is the 3×3 determinant formed from those 9 values.
In this case, the barycentric coordinates are (4/7,2/7,/1/7) and its cyclic rotations, so the 3×3 matrix is a circulant matrix formed by rotating those three. The determinant of a circulant matrix whose first row is (a,b,c) is just a^3+b^3+c^3 = 3abc. Substituting (4/7,2/7,1/7) gives the fraction 1/7.
Similarly, one shows that each of the smaller triangles has fraction 1/21, for a total area of 2/7 for all 4 triangles combined.
There was a typo: the determinant of the circulant matrix is
a^3+b^3+c^3 – 3abc
Solution without ROUTH’s Theorem
One more way
Even easier: