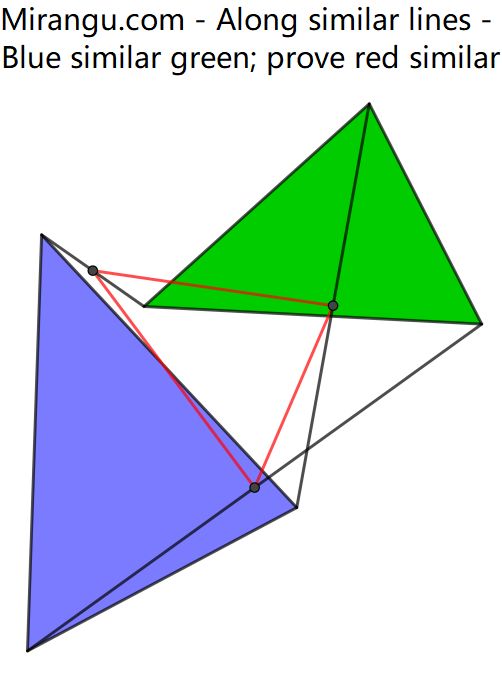
The blue triangle is similar to the green one and has the same orientation. The midpoints between corresponding vertices are connected to form a red triangle. Prove that it is also similar.

Solution

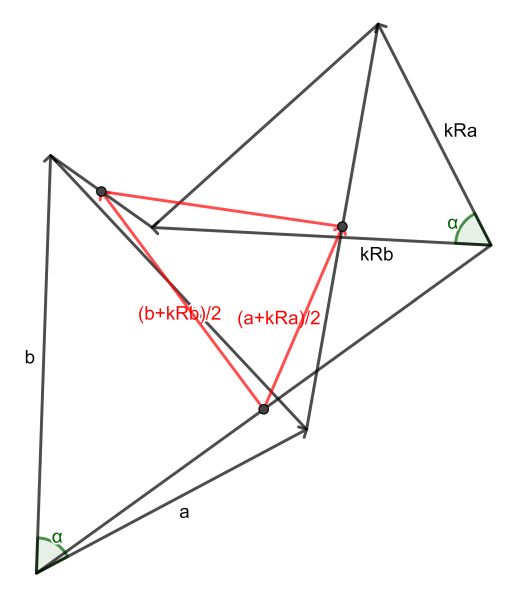
We span the blue and green triangle with vectors a, b and kRa, kRb respectively, where k is a scale factor and R is a counter-clockwise rotation over an angle β.

Now doing some simple vector algebra it is easy to see that the red triangle is spanned by the vectors (a+kRa)/2 and (b+kRb)/2. Let’s first calculate their lengths using the dot product. Using the fact that Ra·Ra=a·a and a·Ra=Ra·a=a·a cos(β), we find that the length of (a+kRa)/2 is K=√(1+k²+2kcos(β))/2 times that of a. The calculation for b gives the same scaling factor K.

Now we take the mutual dot product. Using the fact that Ra·Rb=a·b=|a||b|cos(α) and a·Rb=|a||b|cos(α+β) and Ra·b=|a||b|cos(α-β) we get: (a+kRa)/2·(b+kRb)/2=K²a·b.

We conclude that all three sides of the red triangle have the length of the corresponding blue side times K and hence the red triangle is similar.

Note that the area of the red triangle is K² that of the blue one.

The blue triangle is similar to the green one and has the same orientation. The midpoints between corresponding vertices are connected to form a red triangle. Prove that it is also similar. https://t.co/RzrQaMTOdk pic.twitter.com/WSYeq8FCQ0

— Mirangu (@Mirangu1) March 17, 2023