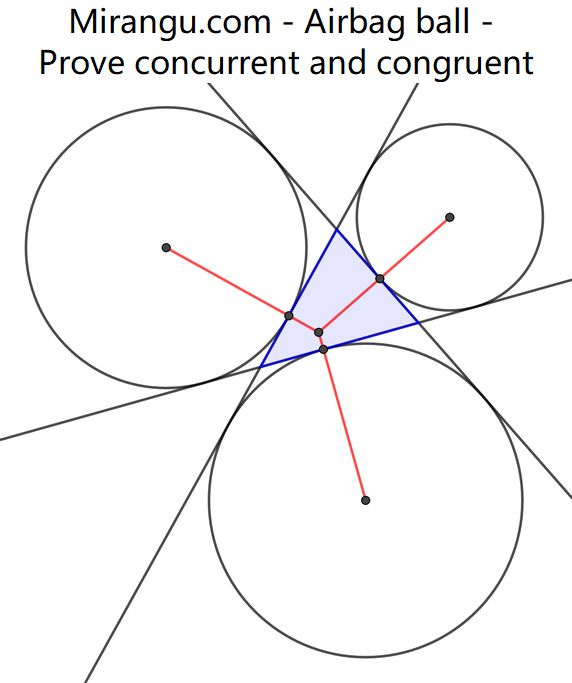
A triangle with its excircles. The tangent radii are extended. Prove that the red line segments are concurrent and congruent.
Scroll down for a solution to this problem.
Solution

Red angles are equal (external bisector) therefore so are the black. Concurrency follows from the trigonometric version of Ceva (maybe there is a simpler way to show this) & the joint apex of the isosceles triangles is the circumcentre of the dashed triangle.
Note that the Pivot Theorem is such an another method to prove concurrence.