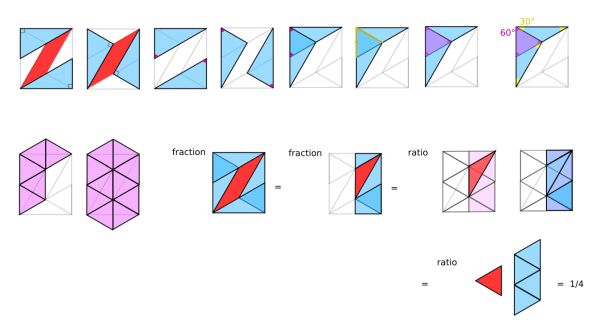
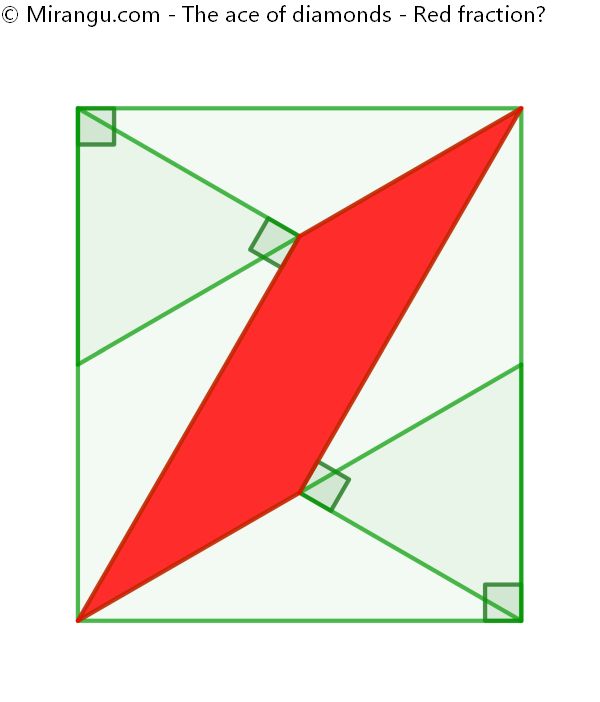
Four congruent right triangles form a rectangle. What fraction is red?
Scroll down for a solution to this problem.
Solution
1/4 of the rectangle is red.
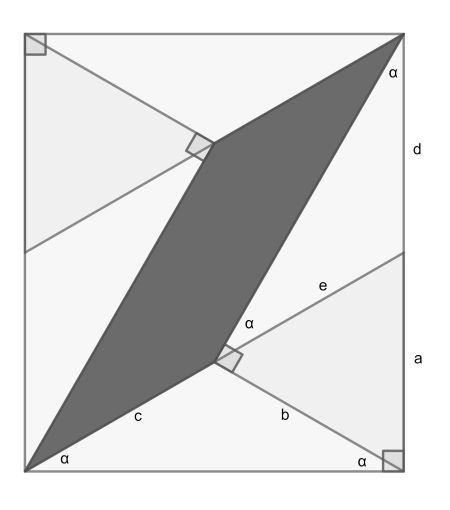
First the triangle with sides a, b and e is isosceles, since a and b both are the short side of one of the four right triangles. Naming the angle α, one can easily propagate it using this fact and the congruency as show. Thus the lower right corner is covered by three isosceles triangles.
Now we can follow the chain a=b=c=d=e. So we have one equilateral triangle and two others of the same size, since α=30°. Setting a=1, their area is √3/4. Since the rectangle has sides √3 and 2, its area is 2√3. It follows that the red area must be √3/2.
Poem
Belladonna kindly composed this geometric poem:
Le vitrail de l’église
Aux carreaux fait la bise
De rouge il est paré
Pour le jour s’allumer
Un peu comme une étoile
Qui doucement largue ses voiles,
Un phénix idéal
Un prodige intégral.
Belladonna

Visual solution
We include a purely visual solution to The ace of diamonds from David Andriana.