A square with its diagonal. Prove that the three red points are collinear.
Distant Alp II
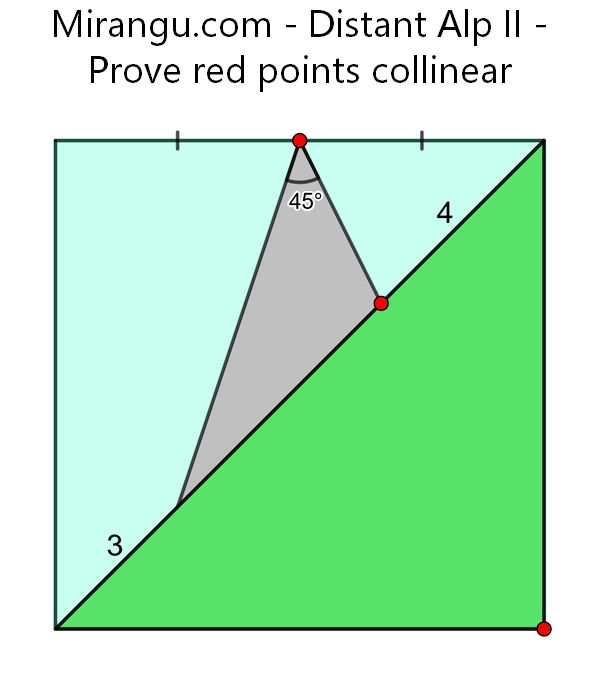

A square with its diagonal. Prove that the three red points are collinear.
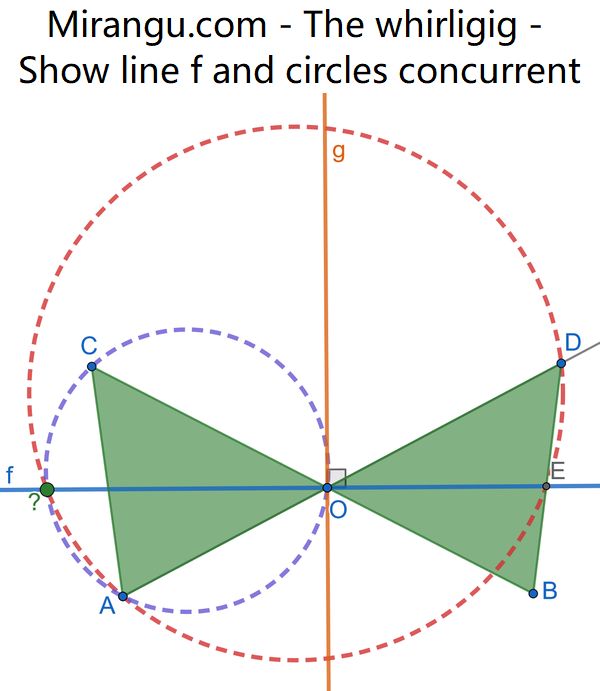
The green blades form a bowtie that is symmetric about the vertical orange line g. Show that the blue horizontal line f, the red circle (ADE), and the purple circle (AOC) are concurrent. (Assume that COB and AOD are colinear.)
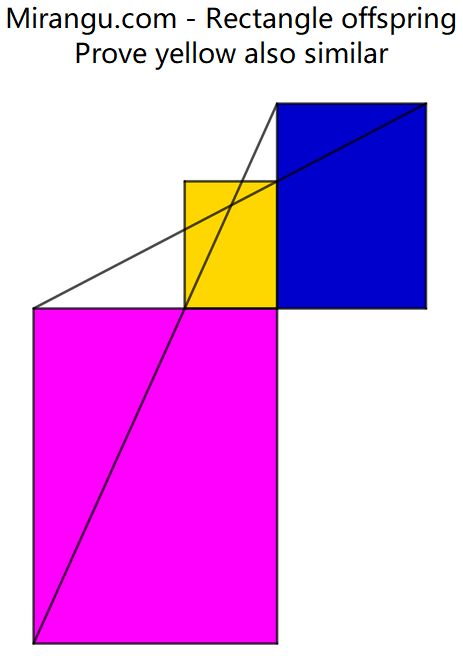
Three rectangles of which the blue and the pink one are similar. Prove that the yellow rectangle is also similar.
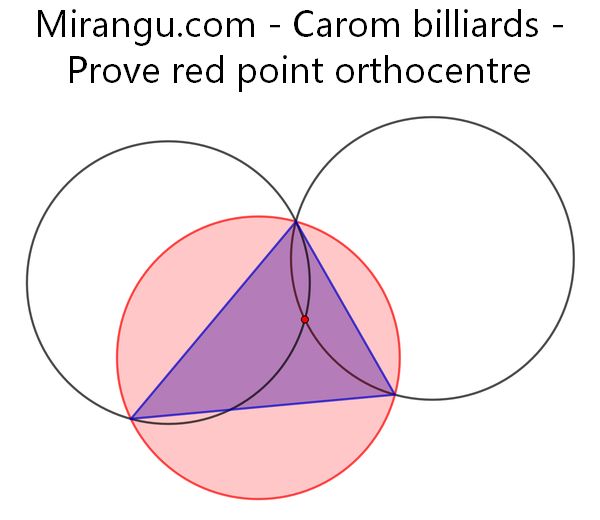
Three congruent circles have a common intersection. Prove that the red intersection is the orthocentre of the triangle.
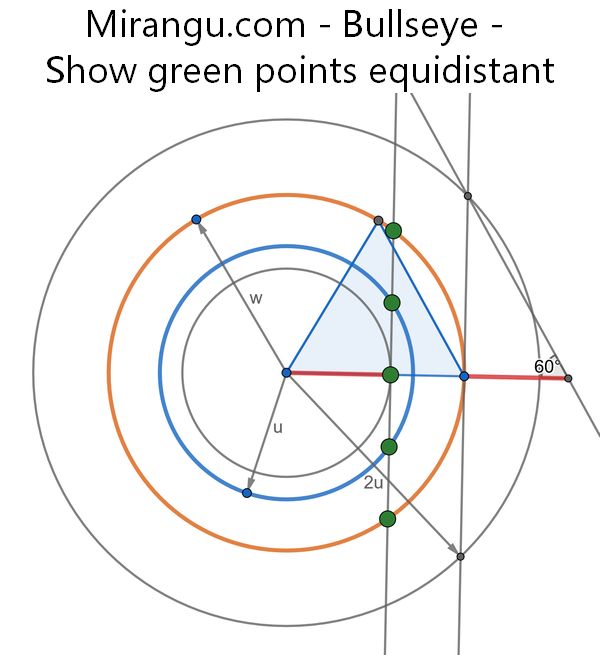
Blue and orange concentric circles intersect a vertical line in green dots. Show that the dots are equally spaced, given that the red intervals shown are of equal length. (The largest circle has radius 2u.)
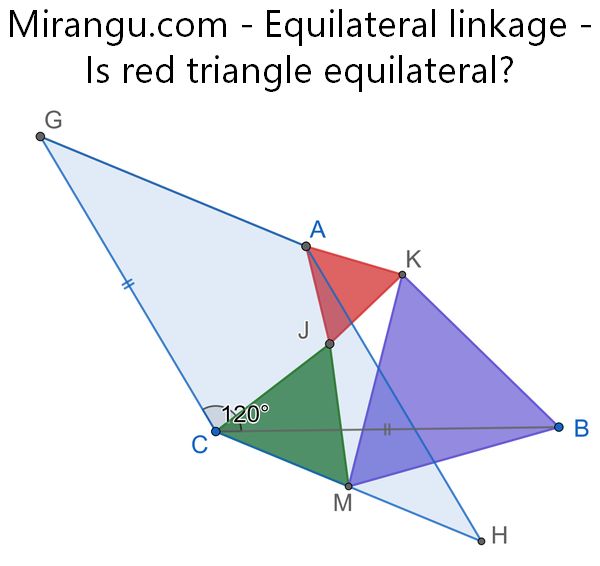
Given 3 points A, B, C, define G so CG=CB and angle GCB is 120 degrees. Define M as the midpoint of side CH of the parallelogram CGAH. The green equilateral has side CM and the purple equilateral has side MB. Is AJK also equilateral?
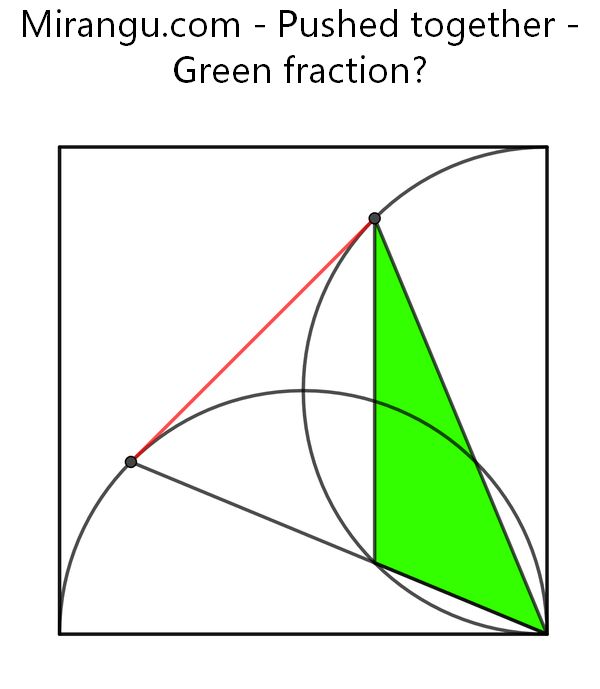
A square containing two semicircles. The red line segment is a common tangent. What fraction is green?
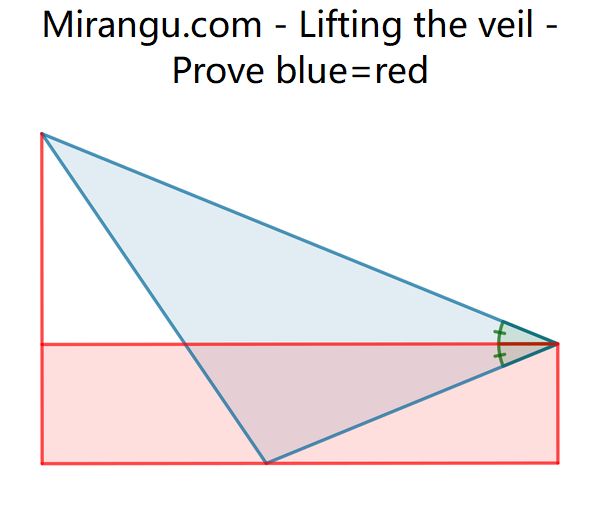
A blue triangle and a red rectangle with an extended side. Prove they have equal area.
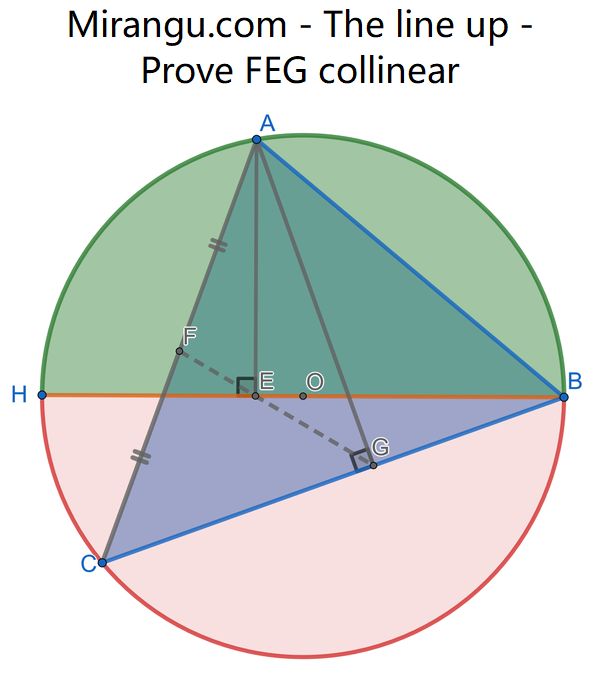
Two semicircles share a common diameter HB. Point A in the upper half projects to E along the diameter, and to G along the line segment BC. F is the midpoint of AC. Show that FEG are collinear.
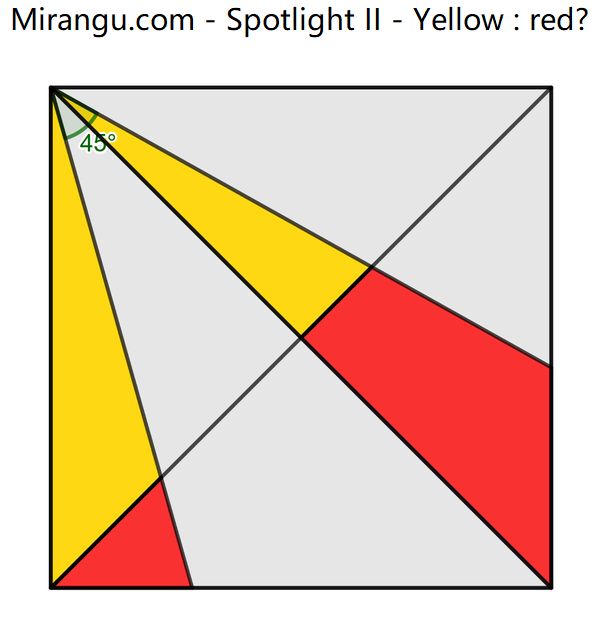
A square is divided in several triangles and quadrilaterals. What is yellow : red?
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now