Two circles, a rectangle and two line segments. Prove that the red points are collinear.
The small cog
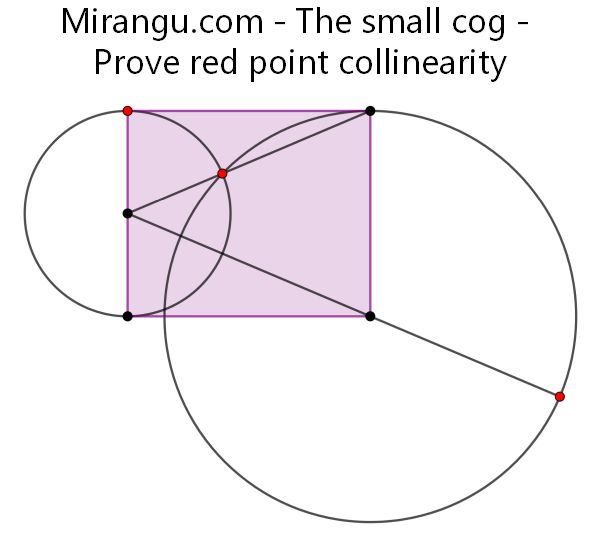

Two circles, a rectangle and two line segments. Prove that the red points are collinear.
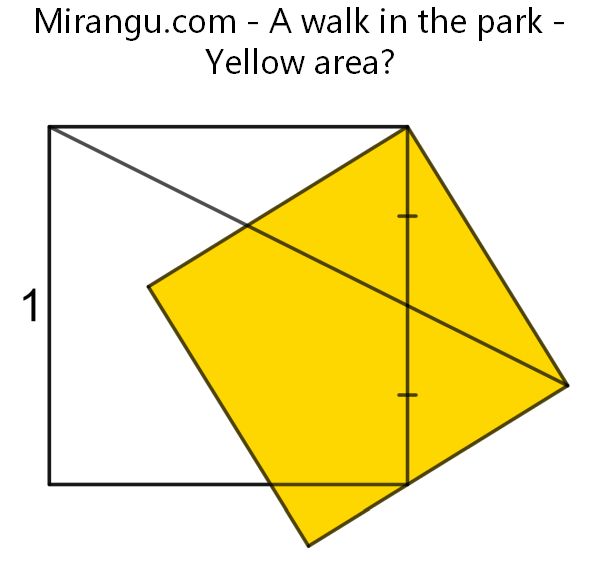
Two squares sharing a vertex and a line segment. What’s the yellow area?
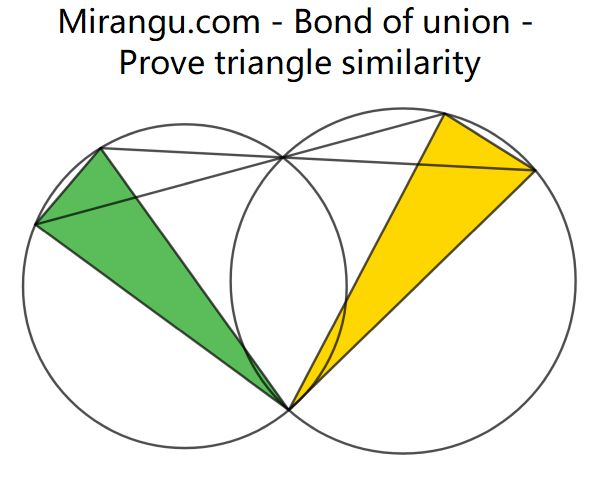
Two intersecting circles with two inscribed triangles and two line segments through an intersection point. Prove that the triangles are similar.
Co-author: Marshall W. Buck.
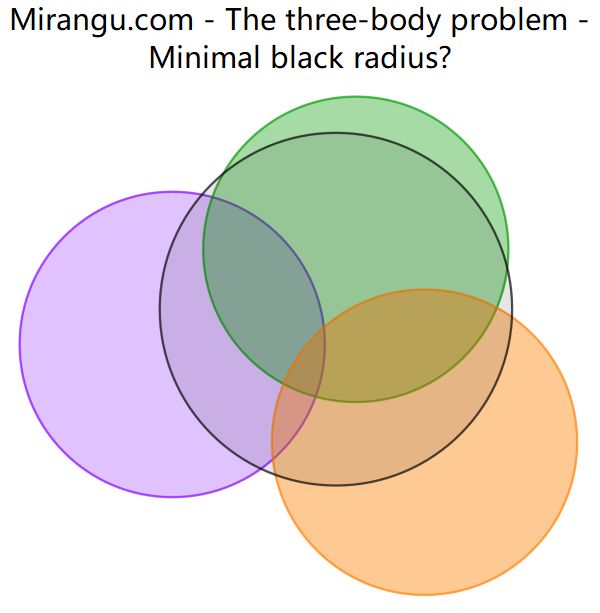
Three coloured unit disks are placed so that they have a common (3-way) intersection, but none of the disks covers the intersection of the other two disks. What is the minimum radius of the disk that would cover all intersections at once, in all cases?
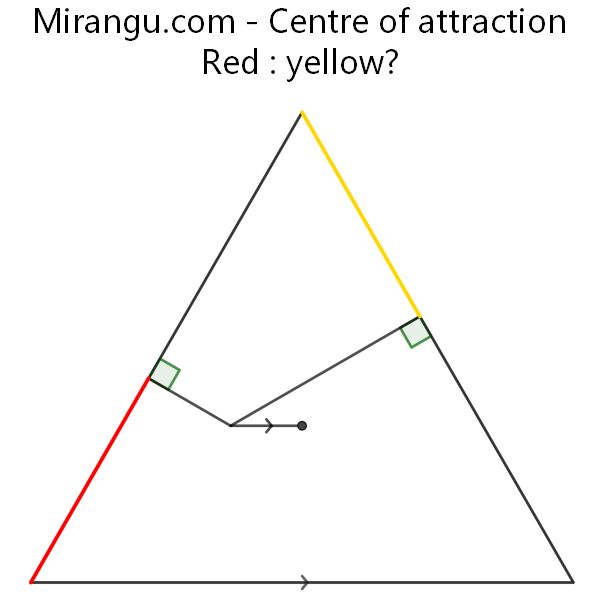
An equilateral triangle with two perpendiculars to a point that is at the same height as the triangle centre. What is red : yellow?
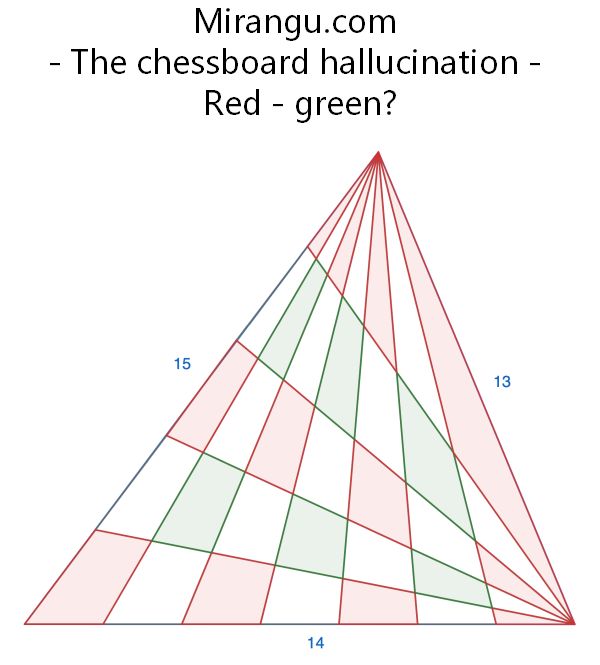
Behold a 13-14-15 triangle. The 15-long side is dissected into 5 equal parts and the 14-long side is dissected into 7 equal parts. What is the difference between the red and green areas?
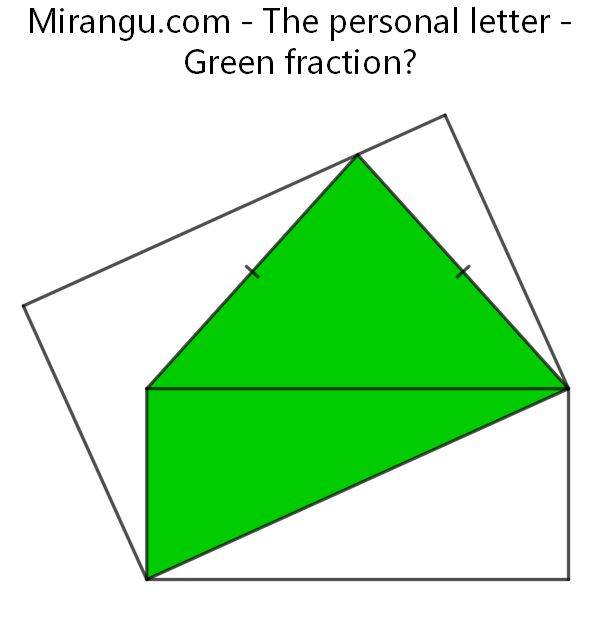
Two rectangles share two vertices. What’s the green fraction?
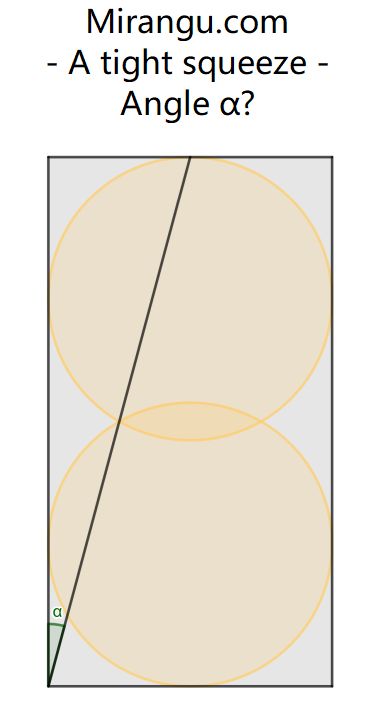
Two intersecting circles inside a rectangle and a line segment connecting vertex, intersection point and tangency point. What’s the angle α?
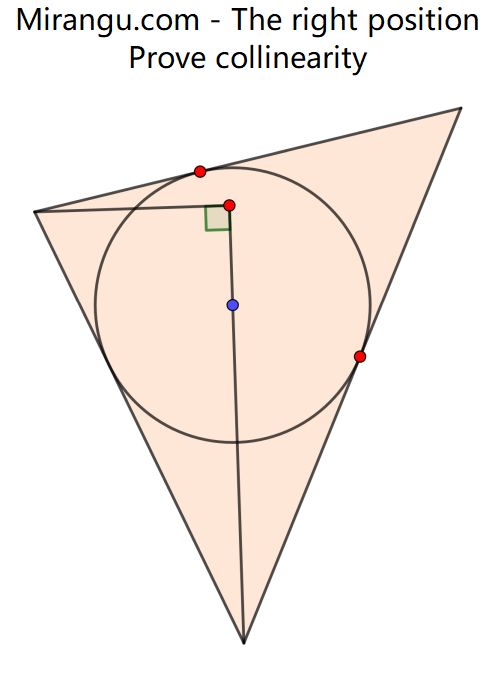
A triangle, its incircle and a right triangle. The circle centre is shown in blue. Prove that the tangency points and right triangle vertex are collinear.
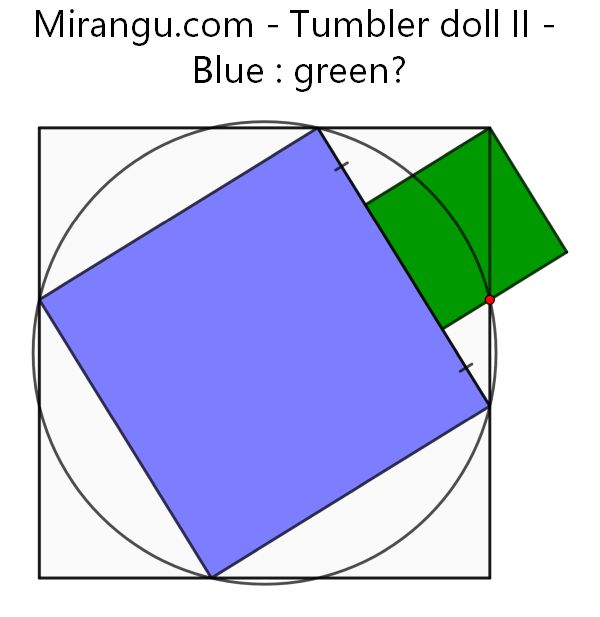
Three squares and a circle. The red point is a common intersection of two square sides and the circle. What is blue : green?
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now