A triangle and its circumcircle. What is red : blue?
Categories
Colour coating
Tag: triangle
Categories
The shadow side
A triangle with sides of length a and c is divided by a cevian of length b. What is brown : yellow in terms of a, b and c?
Categories
Communication across the void
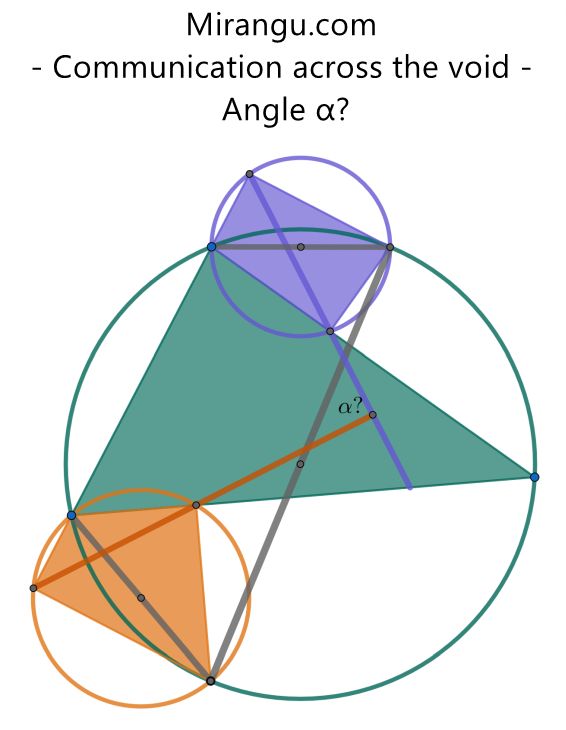
The end points of three diameters of three circles are involved in two cyclic quadrilaterals, purple and orange, separated by the green triangle. What is the angle α between the other (not diameter) diagonals of the two quadrilaterals?
Categories
No vehicles
Two concentric circles and three tangent line segments. If the perimeter of triangle ABC is p, what is the red area?
Categories
Three lawnmowers
Three lawnmowers set off from the three vertices of a triangular field moving clockwise around the boundary. When they reach the next vertex they each take a turn inwards (ie veering to the right of the already cut path ahead) by alpha degrees and then, proceeding in a straight line, all three meet up at a point D inside the field. (They might not all get there at the same time.)
Show that if instead they started out going counter-clockwise and veered left by exactly the same angle alpha at the next vertex, then they would also arrive at a common meeting point H (generally different from D).
Puzzle author: David Odell.
Categories
Slippery slope II
The V is symmetric with respect to the vertical. Prove the algebraic relationship between the various segment lengths indicated by letters.
Categories
Compromise point
The angles ABD and CBD’ are equal. A circle with diameter BD intersects AB and BC at F and H. Show red = blue (FJ = HJ) when J is the midpoint of DD’.
Categories
The cheese flag
Two squares, one of which has an extended side. What is orange : purple?
Categories
Peaucellier pincers
The orange and blue segment lengths are fixed, the pivot point A and the purple line are fixed, and D slides up and down a fixed green line. Show that the intersection point G does not move.
Categories
Doors of perception II
A square, a triangle and a semicircle. The square and the triangle have equal areas. Prove that the triangle incentre is on the square side.