A quadrilateral with two diagonals and an inscribed circle. Prove that the three points are collinear.
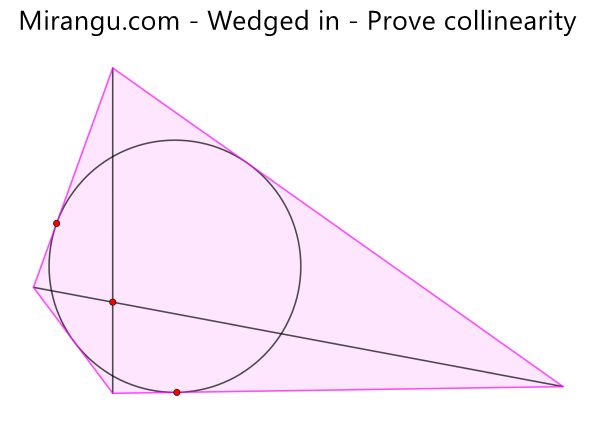

A quadrilateral with two diagonals and an inscribed circle. Prove that the three points are collinear.
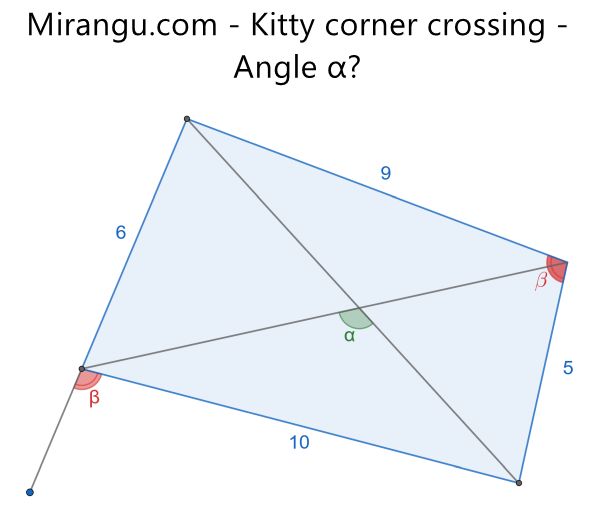
What is the green angle α between the cross ways?

Every side of a quadrilateral is divided into three equal parts. What is purple : orange?
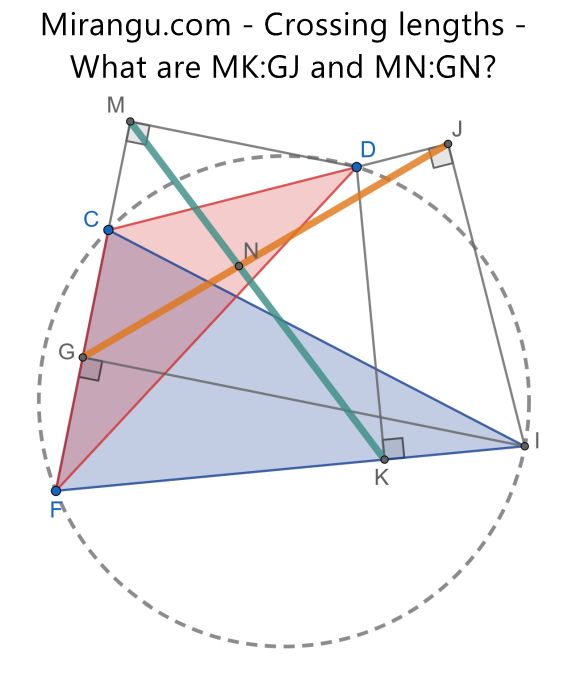
A cyclic quadrilateral (CDIF), where we form two segments: MK (green) with DM perp to FC and DK perp to FI; GJ (orange), with IG perp to FC and IJ perp to CD. What is the ratio MK:GJ ? What about MN:GN?
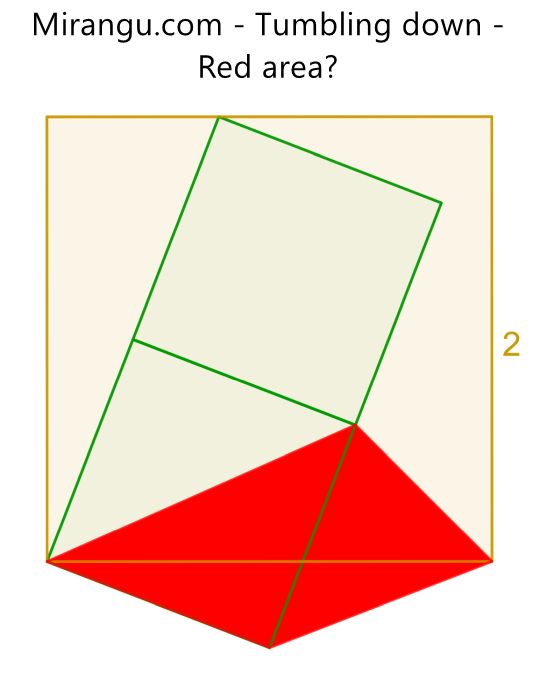
Three squares and a red quadrilateral. What is the red area?
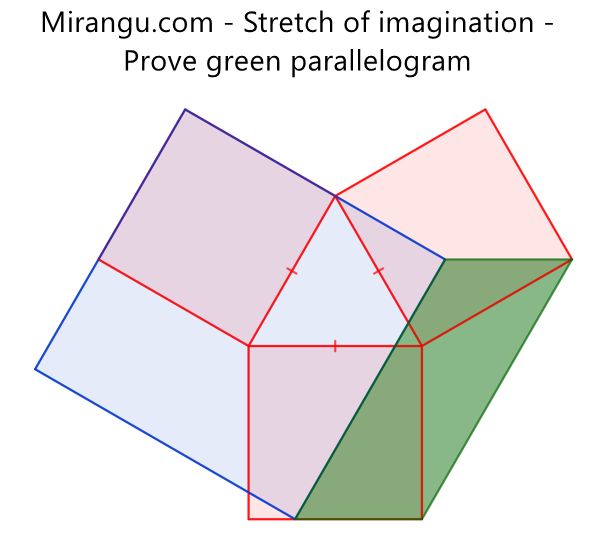
Four squares are placed as shown. Prove that the green quadrilateral is a parallelogram.
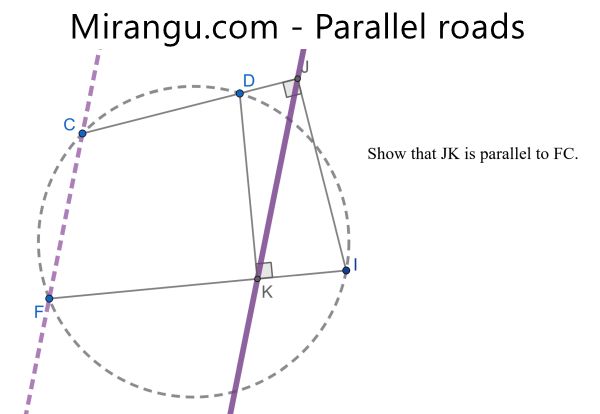
The cyclic quadrilateral FCDI, with points K such that DK perp to FI and J such than IJ perp to CD. Show that JK is parallel to FC.
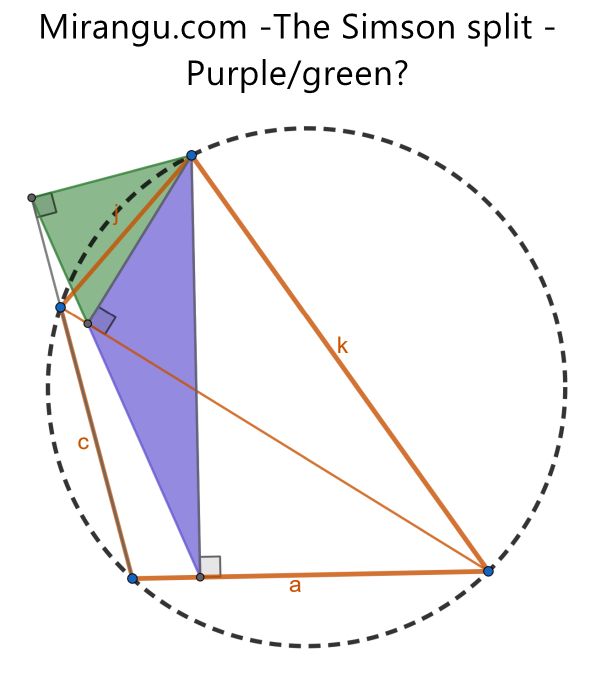
A cyclic quadrilateral has side lengths a, c, j, and k. Three segments drop perpendicularly to two sides and one diagonal of the quad, forming the green and purple triangles between them. What is the ratio purple/green, in terms of a, c, j, k?
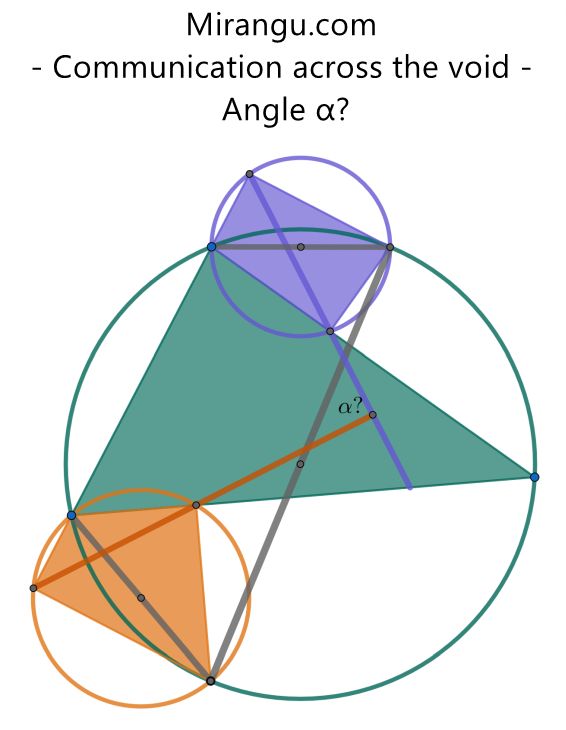
The end points of three diameters of three circles are involved in two cyclic quadrilaterals, purple and orange, separated by the green triangle. What is the angle α between the other (not diameter) diagonals of the two quadrilaterals?
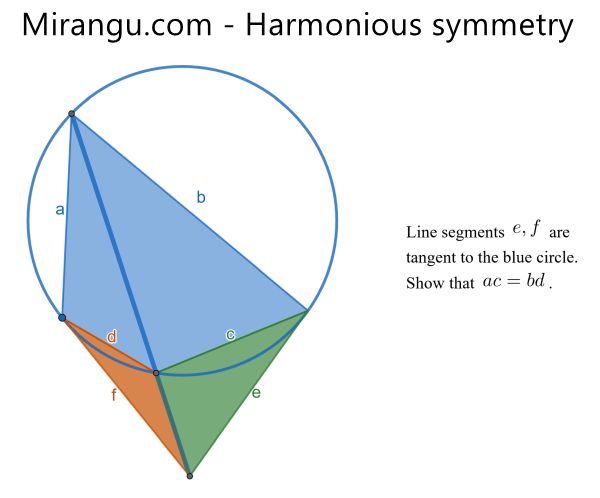
Tangents to a circle intersect, and another line is drawn through that intersection. Show that the products of opposite sides of the blue quadrilateral are equal.
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now