A regular pentagon and two squares. Prove that the four purple vertices are concyclic.
Categories
Squaring the miter
Tag: pentagon
Categories
Eye of Providence
A regular pentagon and an equilateral triangle. What is the angle α?
Categories
Miracle multiplication with pentagons
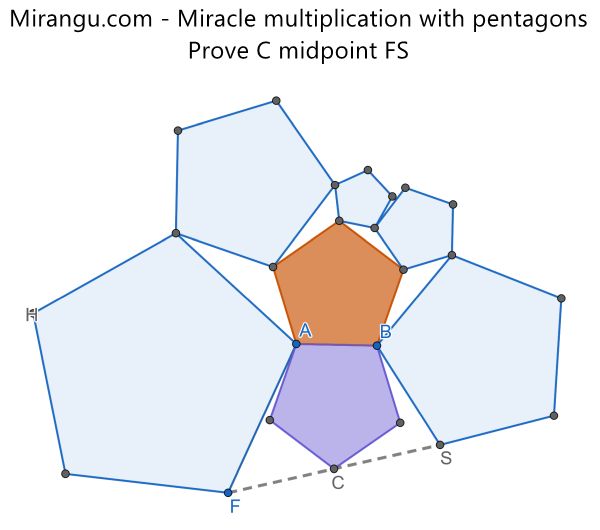
Seven regular pentagons connect as shown. Show that C is the midpoint of the line segment FS.
Categories
Average point constuction
Given a way of finding the midpoint of any segment (and connecting points to make lines, and intersecting lines to get points), construct the average of 5 points, using only 4 midpoint constructions. (Shown is a method using 5.)
Categories
Miquel’s star
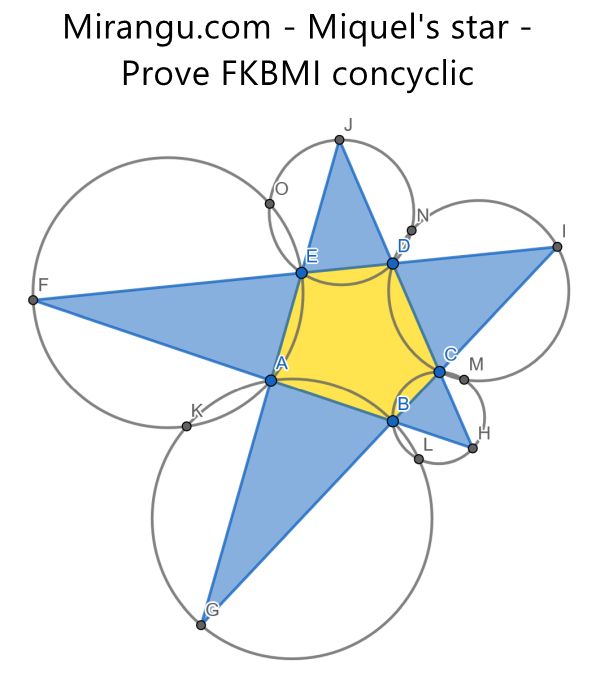
A convex pentagon ABCDE with extended sides and five circles connecting vertices and intersections. Prove that FKBMI are concyclic. Bonus question: prove KLMNO concyclic.
Categories
Centre of attraction II
A square and a regular pentagon share a vertex. The square centre is a vertex of the pentagon. What’s the angle α?
Categories
Meeting in the pentagon
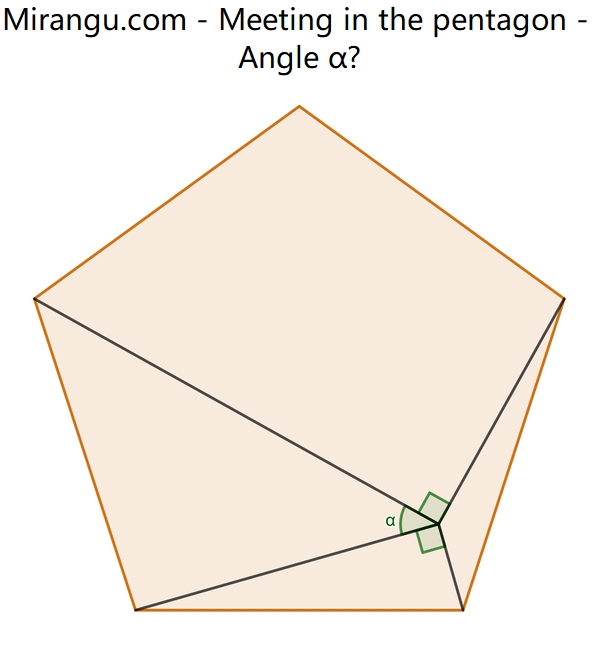
A regular pentagon and two right angles. What is the angle α?
Categories
Circular tension
The orange circle is a locus of points with constant sum of square distances from the vertices of a pentagon ABCDE; I.e., |GA|2 + |GB|2 + …+ |GE|2 is a constant. What is the center of the circle?
Categories
The dumbbell
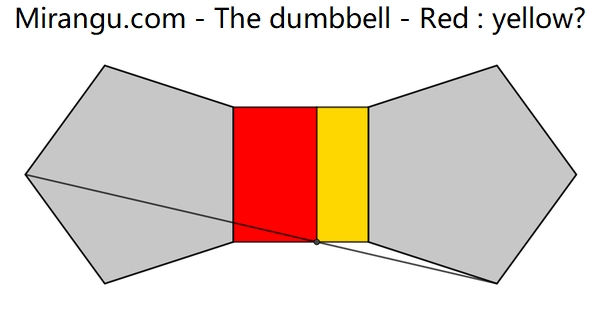
A square and two regular pentagons. What is red : yellow?
Categories
Jacob’s Ladder
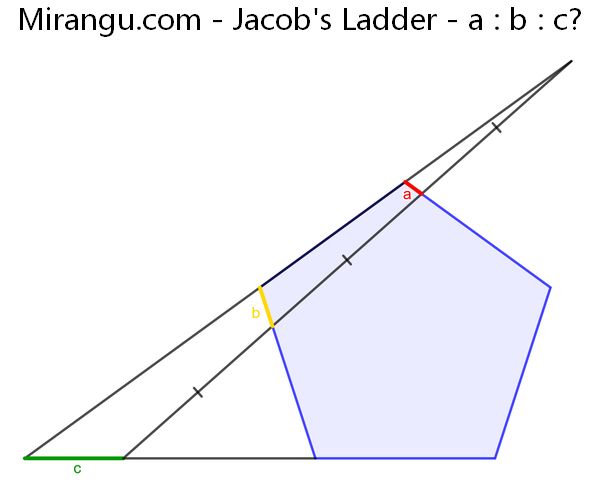
A regular pentagon with two extended sides. What is a : b : c?