A couloured triangle and rectangle with extended sides and two circles. Prove that the triangle and the rectangle have equal areas.
In and out II
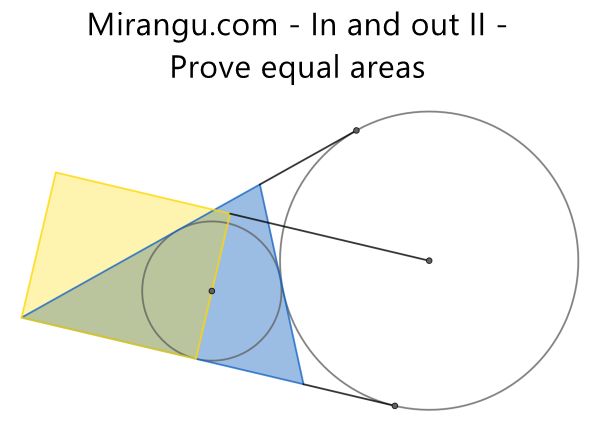

A couloured triangle and rectangle with extended sides and two circles. Prove that the triangle and the rectangle have equal areas.

Orange and Blue disks have a common tangent line IK intersecting DB at A. The red circle has chord DB, and tangents AF and AG. Show that the chord FG , the line DB, and two of the common tangents (LM and OP) have H in common.

An equilateral triangle with a cevian and two inscribed circles. What is yellow : red?
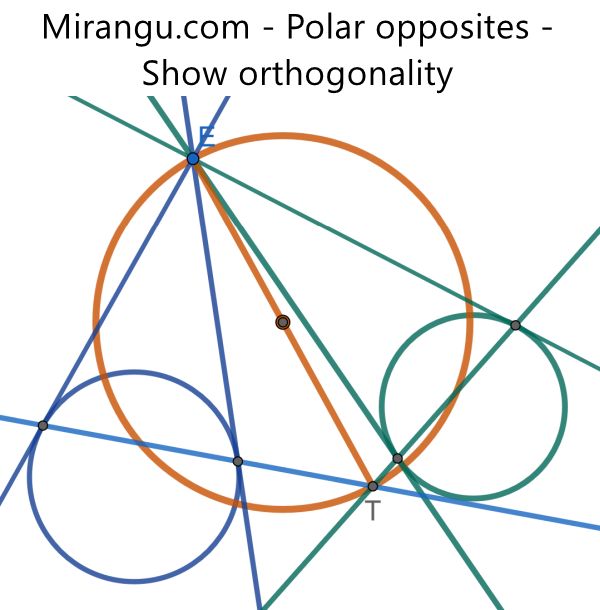
The polar lines for a point E with respect to the blue and green circles intersect at a point T. Show that the orange circle with diameter ET intersects the other circles orthogonally.

A semicircle and two squares. What is the blue area in terms of a and b?
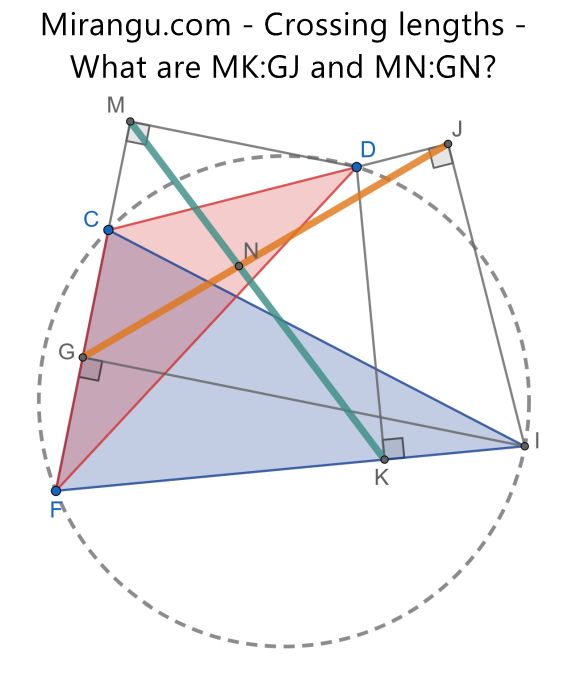
A cyclic quadrilateral (CDIF), where we form two segments: MK (green) with DM perp to FC and DK perp to FI; GJ (orange), with IG perp to FC and IJ perp to CD. What is the ratio MK:GJ ? What about MN:GN?
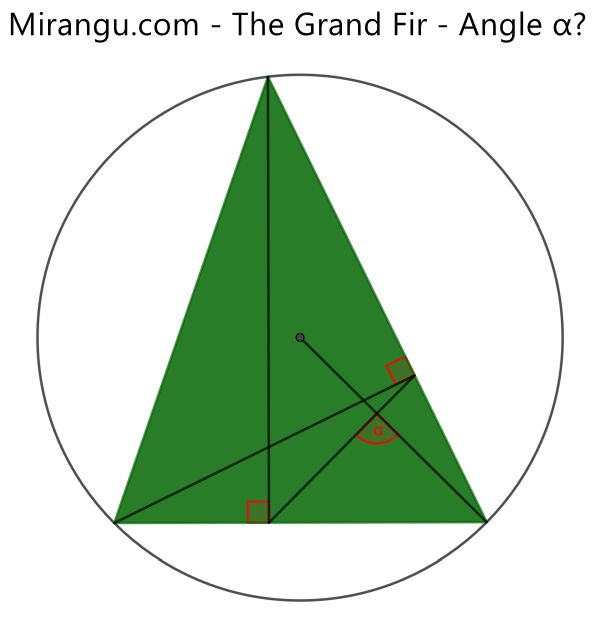
A triangle, its circumcircle, circumcentre and two altitudes. What’s the angle α?

A regular pentagon and two squares. Prove that the four purple vertices are concyclic.

A circle of radius r is interior-tangent to the larger yellow circle of radius R, with diameters overlapping. Express s/k in terms of r and R.
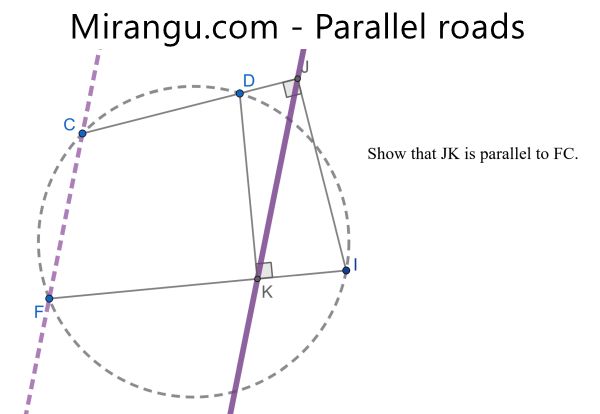
The cyclic quadrilateral FCDI, with points K such that DK perp to FI and J such than IJ perp to CD. Show that JK is parallel to FC.
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now