The end points of three diameters of three circles are involved in two cyclic quadrilaterals, purple and orange, separated by the green triangle. What is the angle α between the other (not diameter) diagonals of the two quadrilaterals?
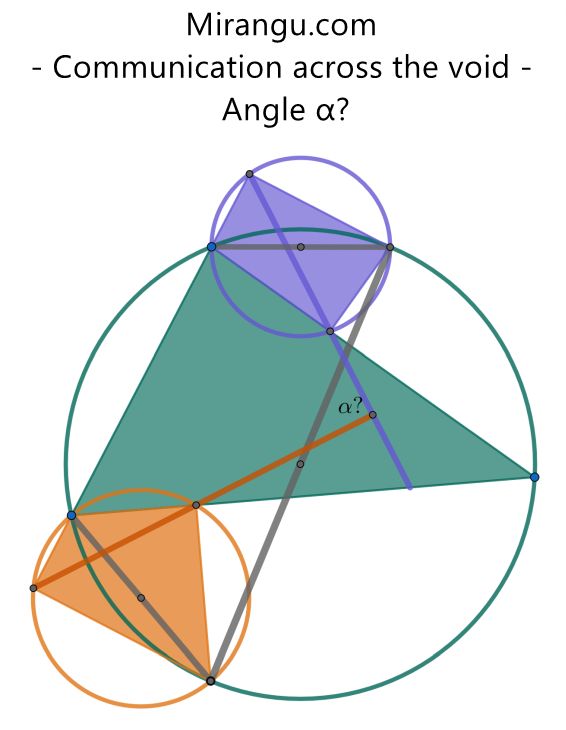
Three lawnmowers set off from the three vertices of a triangular field moving clockwise around the boundary. When they reach the next vertex they each take a turn inwards (ie veering to the right of the already cut path ahead) by alpha degrees and then, proceeding in a straight line, all three meet up at a point D inside the field. (They might not all get there at the same time.)
Show that if instead they started out going counter-clockwise and veered left by exactly the same angle alpha at the next vertex, then they would also arrive at a common meeting point H (generally different from D).
Puzzle author: David Odell.
The V is symmetric with respect to the vertical. Prove the algebraic relationship between the various segment lengths indicated by letters.
A square with two line segments. What’s the angle α?
The angles ABD and CBD’ are equal. A circle with diameter BD intersects AB and BC at F and H. Show red = blue (FJ = HJ) when J is the midpoint of DD’.
The orange and blue segment lengths are fixed, the pivot point A and the purple line are fixed, and D slides up and down a fixed green line. Show that the intersection point G does not move.
Three equilateral triangles enclose three interior triangles that share a common angle size α. The outer triangles have areas s1, s2, and s3, the inner have areas t1, t2, t3. Express the ratio t1: t2: t3 in terms of s1, s2, s3.
Show that the red-blue line is perpendicular to the base line.
Two squares and an extended side. What’s the angle α?
Two angle bisectors and an exterior angle bisector for ABC form a second triangle DHE. Green perpendicular lines from E to AC and D to AB meet at I. J is the circumcenter of ABC. How are H, J, and I related?
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now