Three regular hexagons inside a circle. Two shared vertices and five vertices on the circle. What’s red : green?
Tomba La Bomba


Three regular hexagons inside a circle. Two shared vertices and five vertices on the circle. What’s red : green?
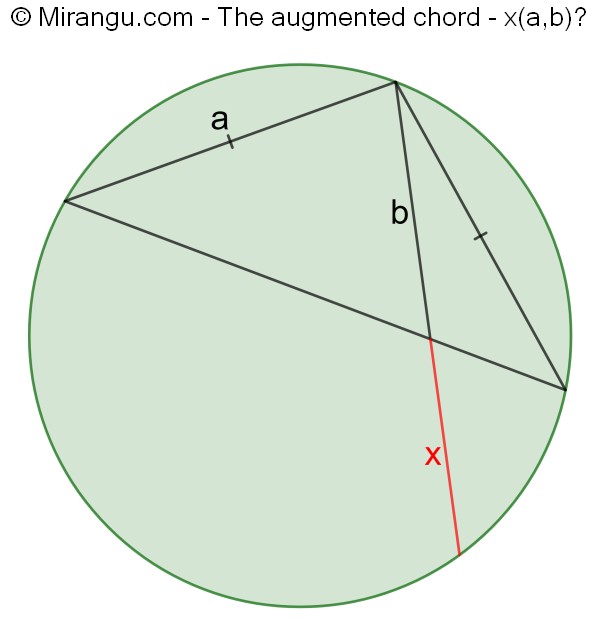
A circle with four chords. What is the length of line segment x in terms of lengths a and b?
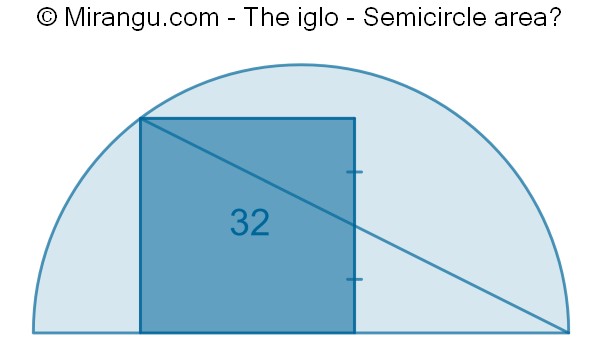
A semicircle, a square and a chord. If the square has area 32, what is the semicircle area?
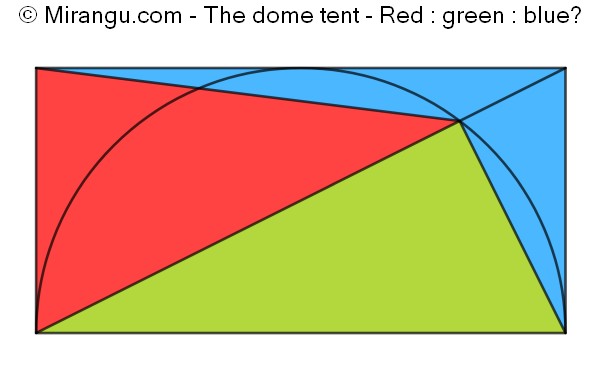
A rectangle with a diagonal and an inscribed semicircle. What is red : green : blue?
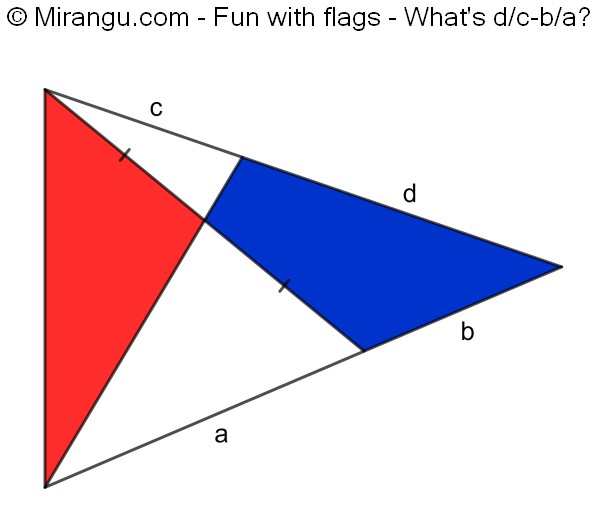
A triangle with two cevians. What is d/c-b/a?
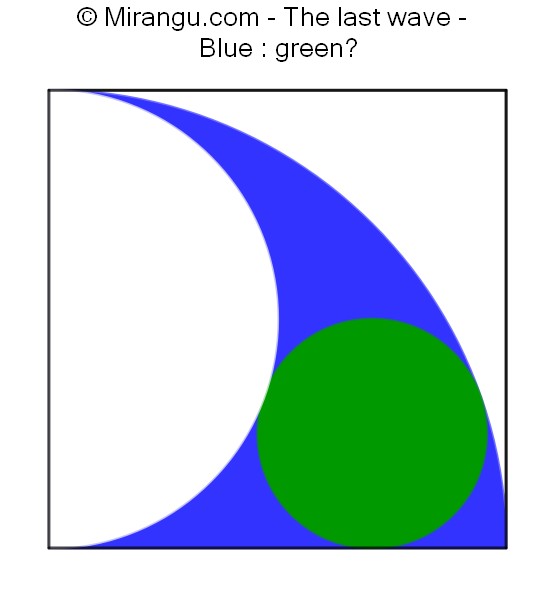
A square containing a quarter circle, a semicircle and a circle. What is the proportion blue : green?
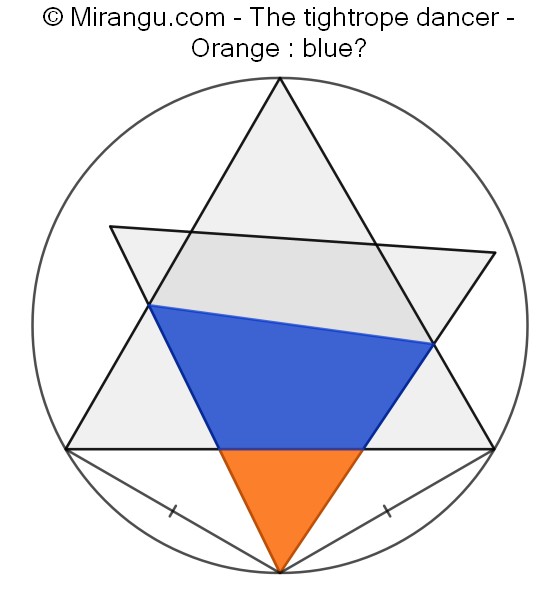
A circle containing an isosceles and two equilateral triangles. What is the proportion orange : blue?
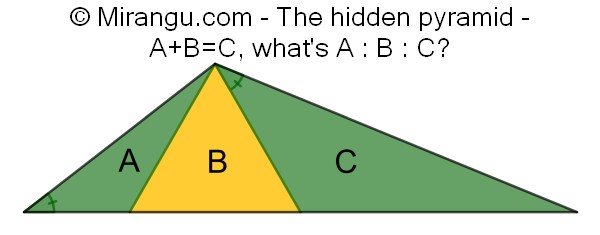
A triangle with an inscribed equilateral triangle. If areas A and B add up to C, what are the proportions A : B : C?
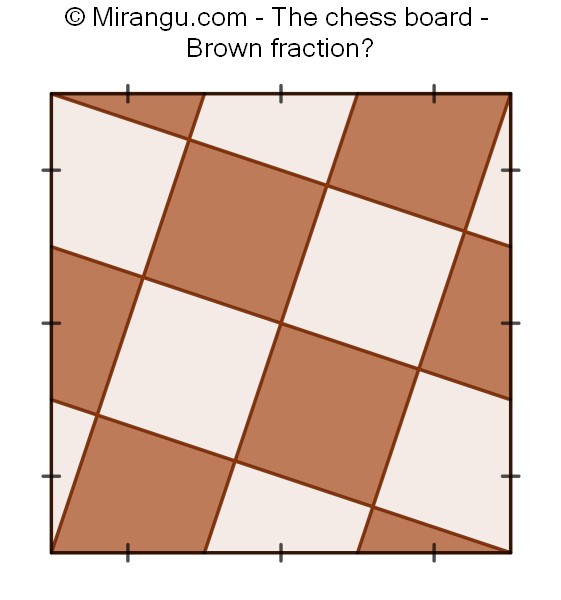
A square is divided by six line segments. What fraction is brown?
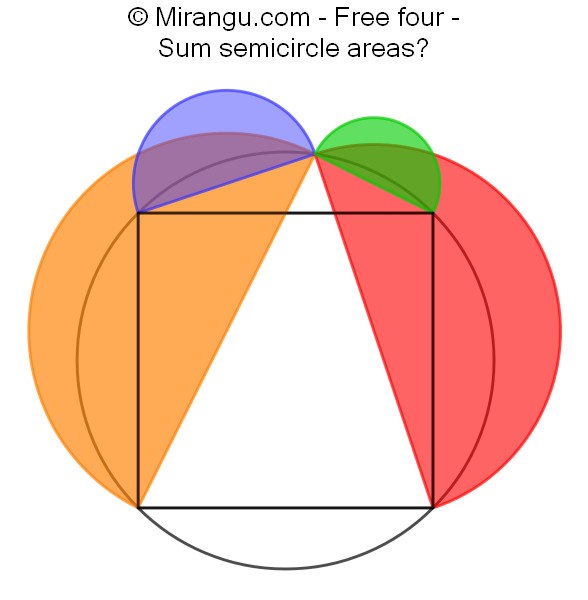
A unit circle with an inscribed square and four semicircles. What’s the sum of the semicircle areas?