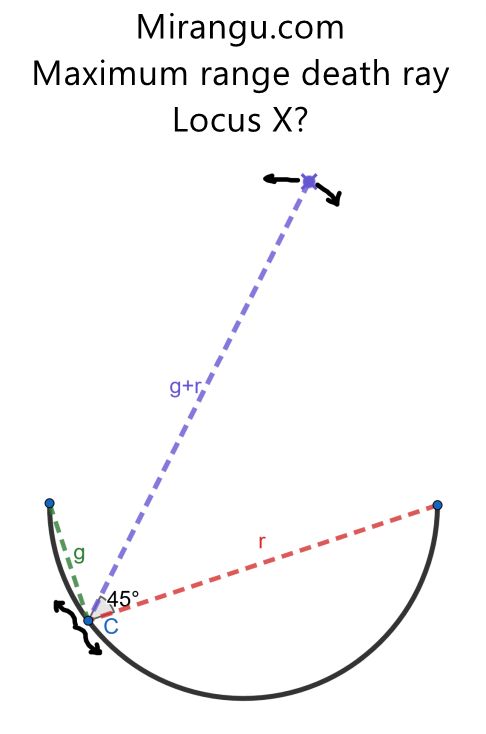
The death dish is semicircular, with point C for aiming the ray, which bisects the green and red lines. The maximum range of the death ray is the sum of the red and green lengths. What is the locus of the maximum point X as C varies?
Scroll down for a solution to this problem.
Solution
It is a semicircle with radius √2-1 times the death disk radius.

Use Ptolemy’s theorem for quad BCAF. Here it gives FA*BC+BF*CA=BA*CF and with BF=FA=BA/sqrt(2) we get CF=(g+r)/sqrt(2)). Of course, F is the center of homothety: CE bisects angle BCA -> it intersects (BCA) 2ndly in F s.t. BF=FA.
More solutions: https://x.com/Mirangu1/status/1885236900337692905
One reply on “Maximum range death ray”
Problems of the type “what is the locus traced by point X as …. etc.” appear harder than our usual problems. My hypothesis for why this is: usually one can “see” in a diagram certain things that help one to prove the result. Points line up, or angles appear to be 90 degrees, etc. These inductive hypotheses can be proven, and then the final result. For loci problems, one needs first to construct a few points on the curve before guessing what the curve is, before trying to prove it. Users of geogebra, or the like, are well equipped for this undertaking. They can simply mark the point X with “Trace ON”, and click “animate” on some other point of the construction. This provides a movie of the process and a trace of the locus.