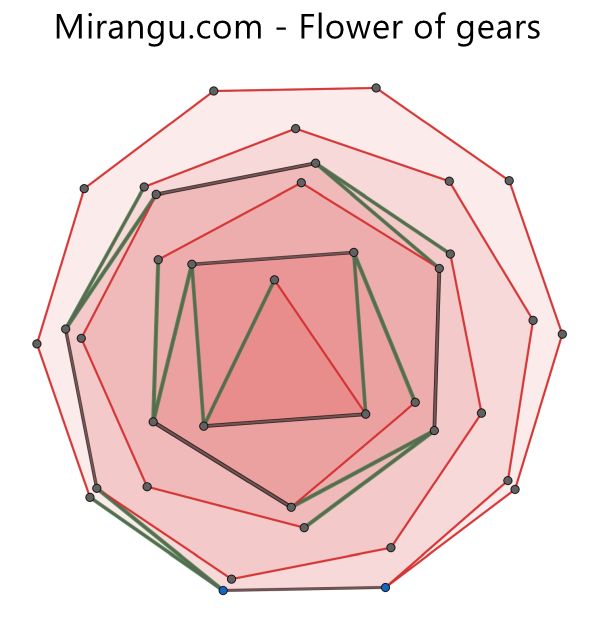
During one step every internal polygon rotates to the next position along its outer polygon, merging two green sides. How many full turns are made by the innermost triangle before the entire configuration returns to its initial state?
Scroll down for a solution to this problem.
Solution
The triangle makes 588 turns.

More solutions: https://x.com/Mirangu1/status/1935955625092977114
One reply on “Flower of gears”
Bob Ruyle points out elsewhere that if we disregard whether the n-gons have turned from their original position when they return to their original “space”, then, in fact, the configuration returns after only 10 turns. The triangle turns (1/3-1/10)=7/30 of a turn per step, so would turn only 7/3 of one complete turn, instead of the 588 turns required to bring all the sides back to their starting positions.