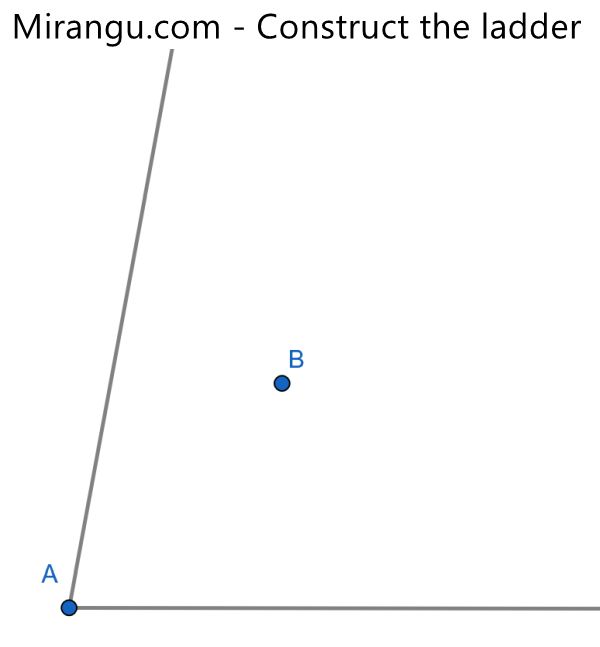
Two rays emanating from point A and a point B between them. Construct the line segment that has an endpoint on each ray and its midpoint in B using a tool such as GeoGebra, explaining your steps.
Scroll down for a solution to this problem.
Solution

With GeoGebra, draw a line through B parallel to the baseline, intersecting the sloped line from A at E. Use the “Dilate From Point” tool to dilate E from point A to the point E’. (Or use the “Circle with Center” tool to draw a circle with center E, containing A and E’.) Connect E’ to B and extend to a ray, intersecting the baseline at F. Then E’ and F are the desired points, with B as their midpoint.
More solutions: https://x.com/Mirangu1/status/1920078671550824479
2 replies on “Construct the ladder”
idea: Complete A and the rays to a parallelogram with B as center of symmetry:
Using GeoGebra 6 classic and “Reflect Object in Point”:
Reflect the two given rays in B. The intersection points of the new rays with the given are the endpoints of the “Ladder”.
Detailed see below.
Sorry again: The Text below “Reflect Object in Point” has to be
Click at ray f and then at B to get ray f ‘;
click at g and then at B to get ray g’.