Three discs have one 3-way common point on their boundaries. Where do the red rays intersect? How are the points of intersection related to the common boundary point?
When worlds collide
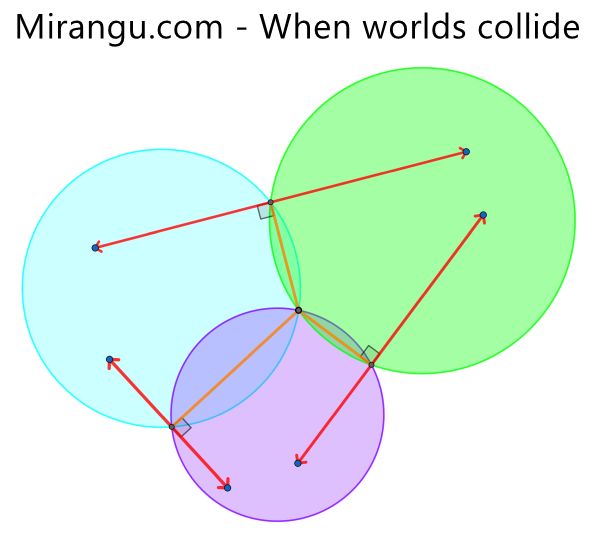

Three discs have one 3-way common point on their boundaries. Where do the red rays intersect? How are the points of intersection related to the common boundary point?
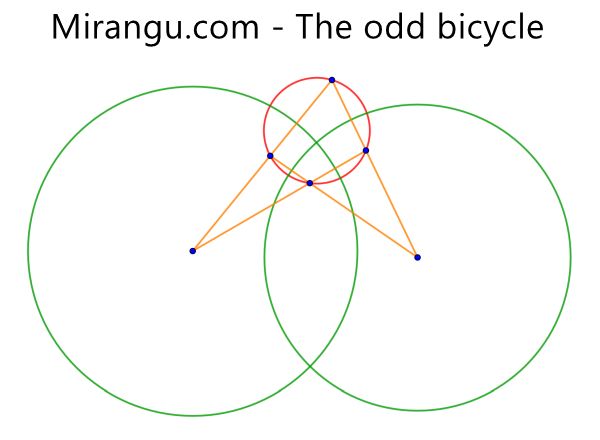
Three circles (two with centre) and four line segments. Prove that, if the small circle is orthogonal to both wheels, then the wheels are also orthogonal to each other.
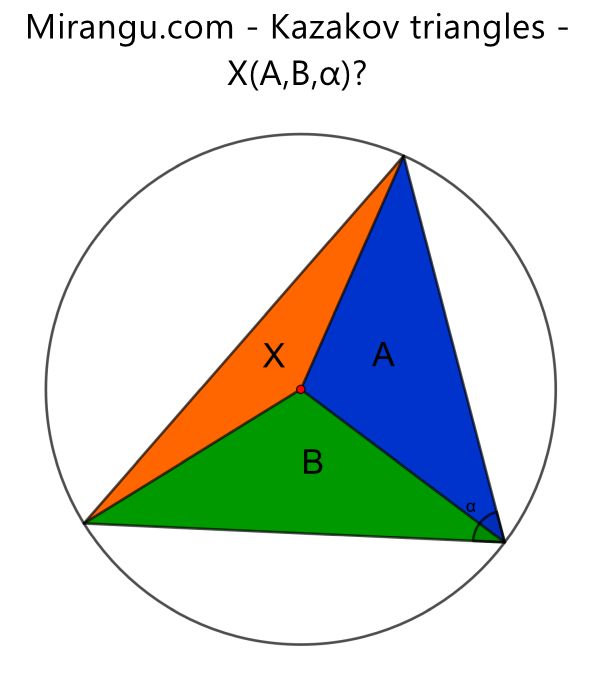
A circle with its centre and three triangles consisting of chords and radii. Express area X in terms of A, B and α.
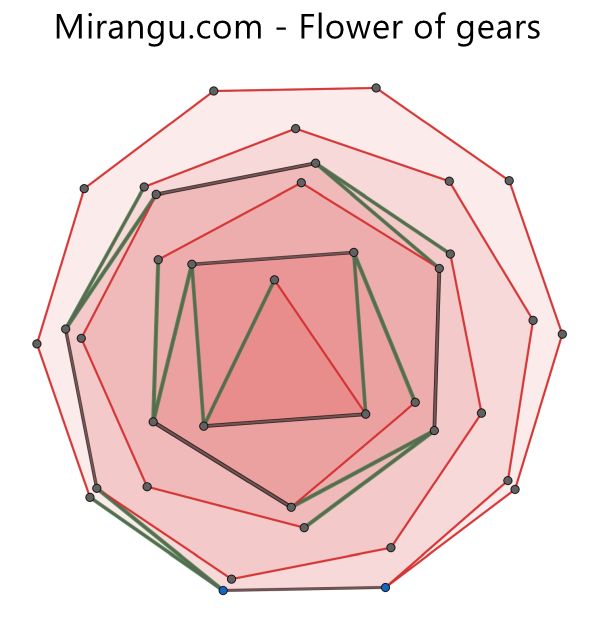
During one step every internal polygon rotates to the next position along its outer polygon, merging two green sides. How many full turns are made by the innermost triangle before the entire configuration returns to its initial state?
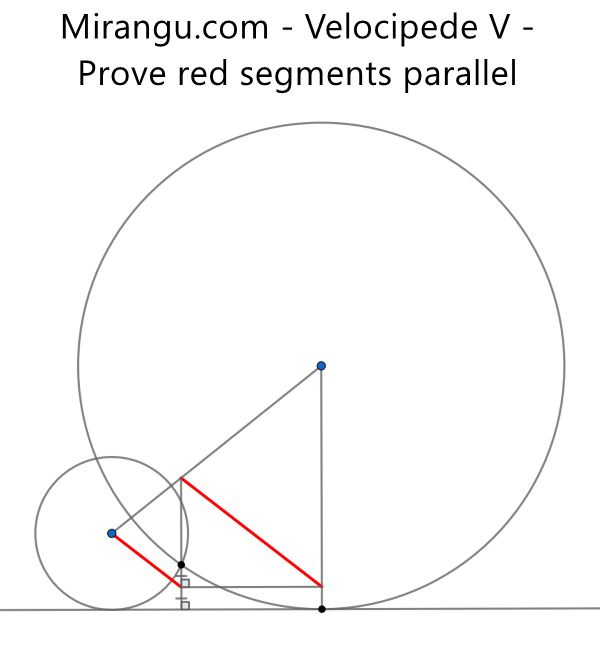
Two circles, a common tangent and several line segments. Prove that the red line segments are parallel.

The left wall of a rectangular pit can slide frictionlessly along the floor. An inward force of F is needed to maintain the position of the 6 congruent circles, but a larger force G is needed to push the walls inward, lifting the circles. What is G/F?
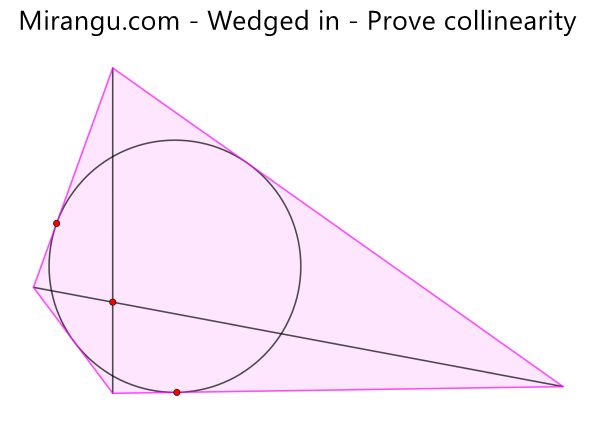
A quadrilateral with two diagonals and an inscribed circle. Prove that the three points are collinear.
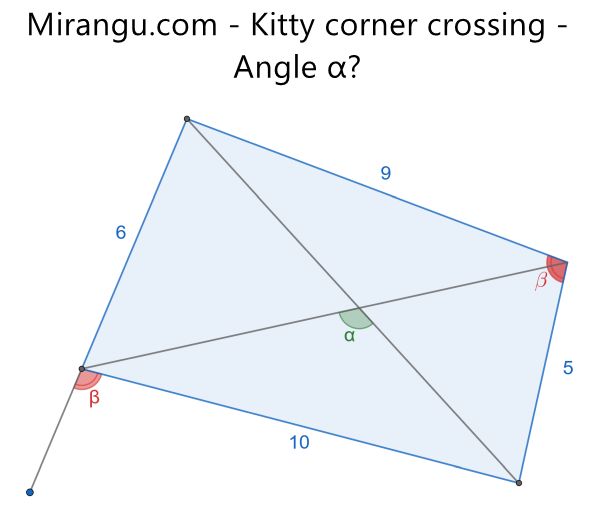
What is the green angle α between the cross ways?

A triangle with its incircle and a cevian. What is red : yellow?
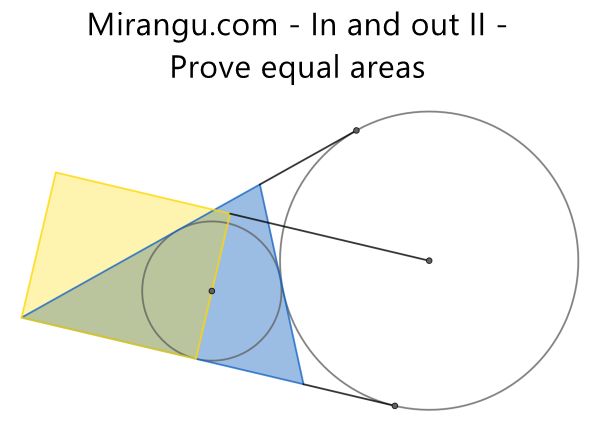
A couloured triangle and rectangle with extended sides and two circles. Prove that the triangle and the rectangle have equal areas.
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now