Three circles (two with centre) and four line segments. Prove that, if the small circle is orthogonal to both wheels, then the wheels are also orthogonal to each other.
The odd bicycle
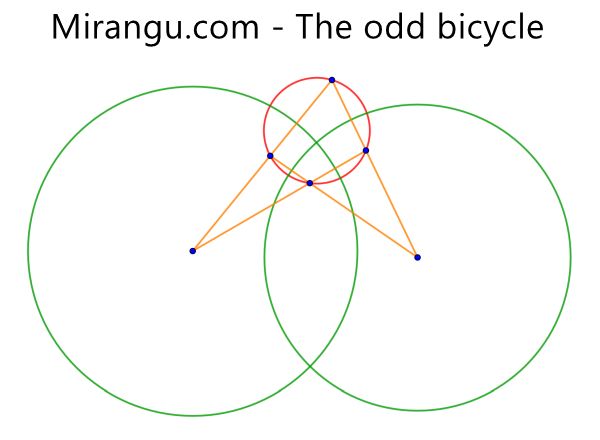

Three circles (two with centre) and four line segments. Prove that, if the small circle is orthogonal to both wheels, then the wheels are also orthogonal to each other.
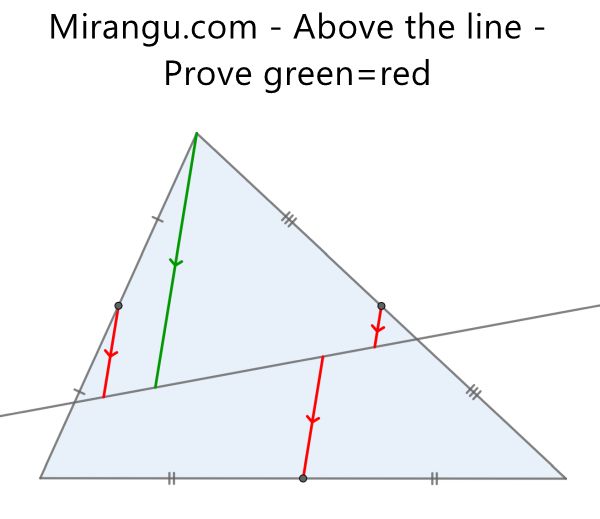
A triangle cut by a line and four parallel line segments. Prove that green = red.
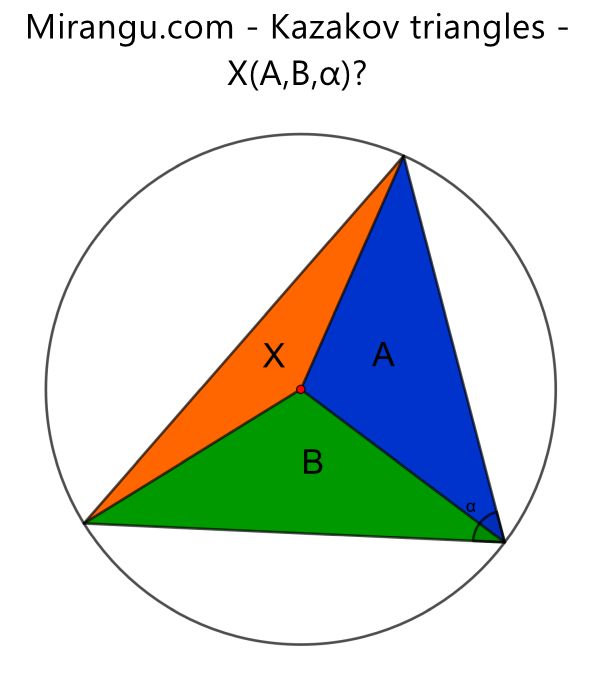
A circle with its centre and three triangles consisting of chords and radii. Express area X in terms of A, B and α.
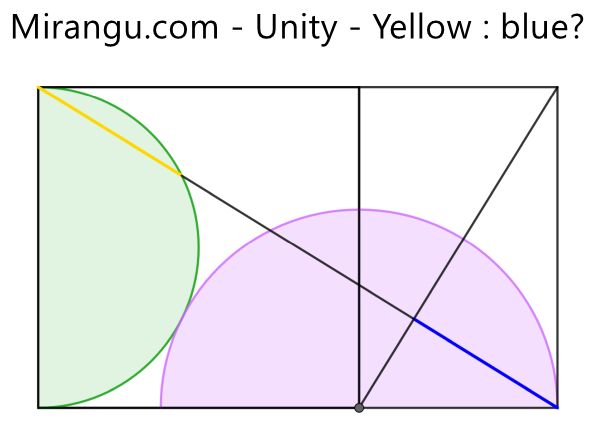
A square, a rectangle and two semicircles, one of which is centered in the shared vertex. What is yellow : blue?
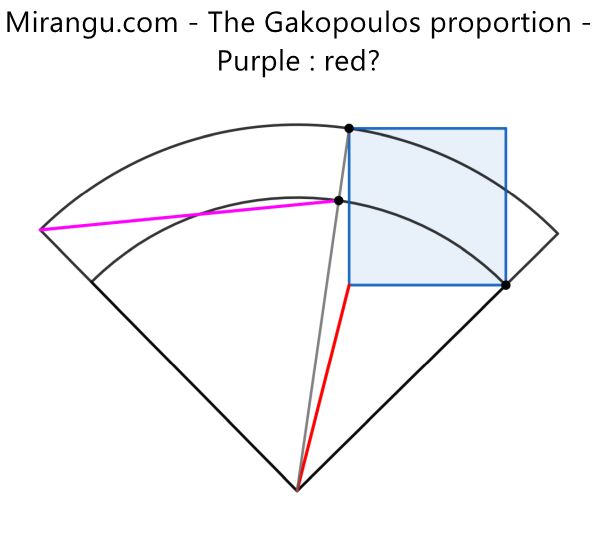
Two concentric quarter circles and a square. What is purple : red?
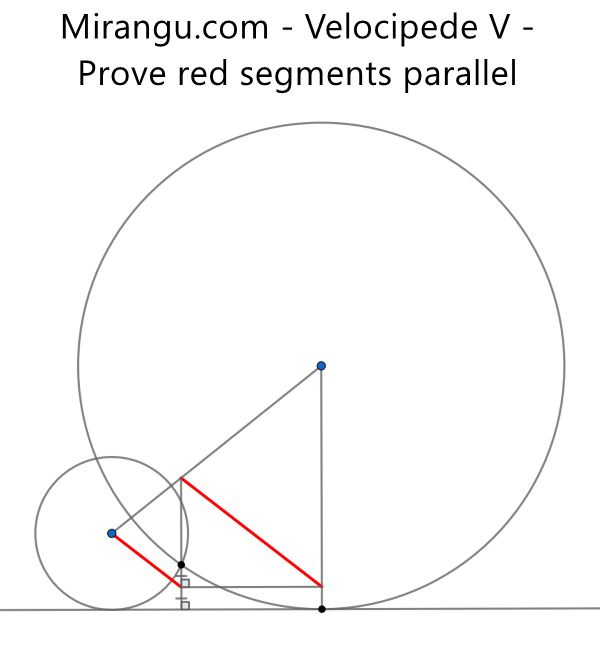
Two circles, a common tangent and several line segments. Prove that the red line segments are parallel.
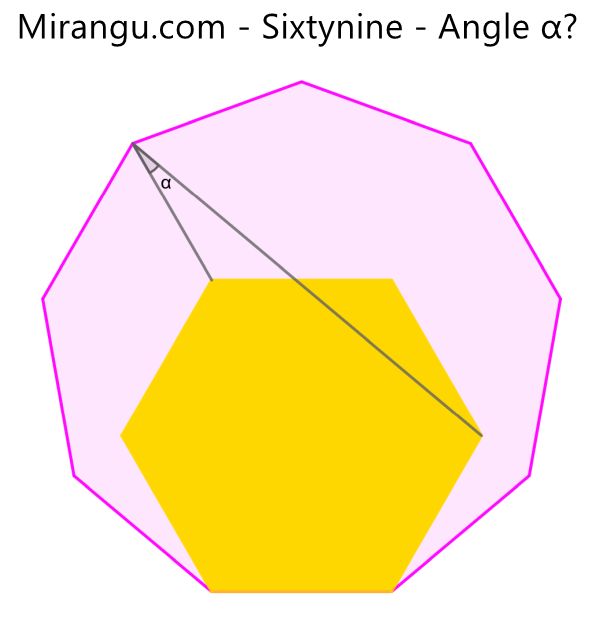
A regular hexagon shares a side with a regular nonagon. What’s the angle α?
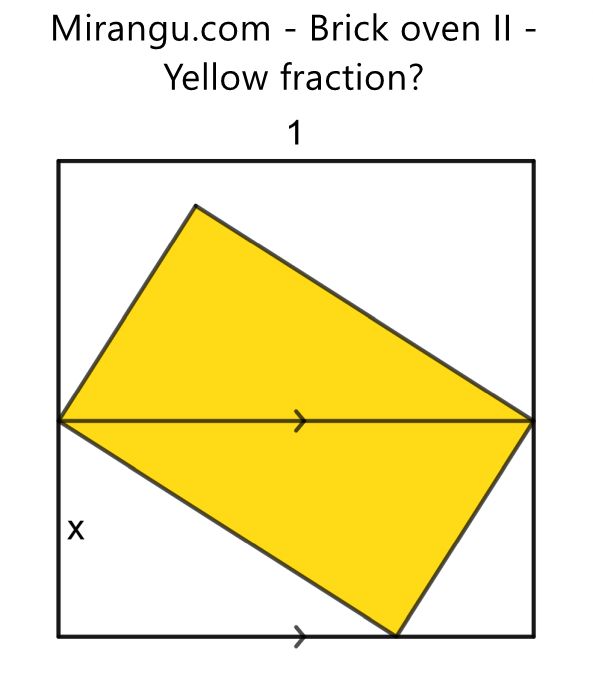
A rectangle inside a square. What fraction is yellow in terms of x?
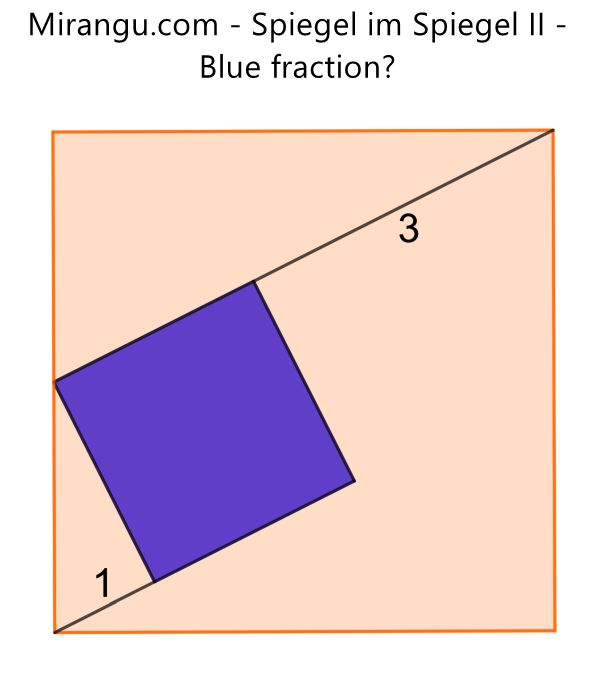
A square containing a square with two extended sides. What is the blue fraction?
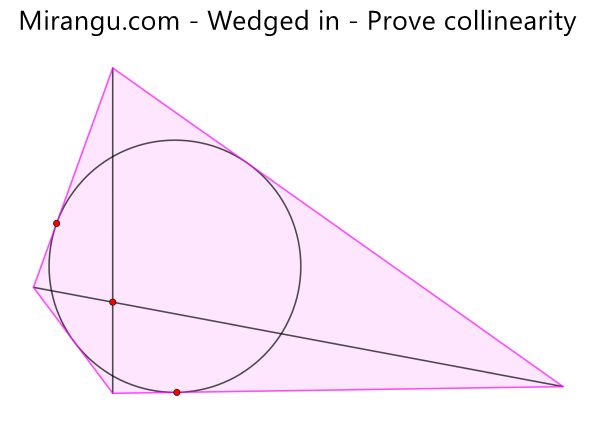
A quadrilateral with two diagonals and an inscribed circle. Prove that the three points are collinear.
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now